Алгоритмы обработки двумерных массивов
Двумерный массив - это структура однотипных элементов, расположенных в виде таблицы значений. Такое представление значений соответствует математическому понятию двумерный массив. Каждый элемент в двумерном массиве идентифицируется номером строки и номером столбца, на пересечении которых он расположен. Например, в двумерном массиве А, изображенном на рис. 34, элемент со значением 5 расположен на пересечении третьей строки и второго столбца. Этот элемент будет обозначаться как А(3,2). А элемент А(1,4) имеет значение , равное нулю. Такое представление набора значений позволяет выполнять обработку как отдельных значений в двумерном массиве, так и последовательности значений, расположенных в строках или столбцах.В дальнейшем будем считать, что для двумерного массива A(N,М) в обозначении элемента А(i,j) первое значение i соответствует номеру строки и изменяется от1 до N, а j - номеру столбца и изменяется от 1 до М. В отличие от одномерного массива, в котором использовался только один номер для определения местоположения элемента и требовался только один цикл для ввода элементов, в двумерном массиве для обработки элеменов необходимы два вложенных друг в друга цикла. Внешний цикл предназначен для изменения номера строки i, а второй, внутренний, - для изменеия номера столбца j в текущей строке i.
На рис. 35 представлен простой алгоритм ввода элементов, построенный в виде структуры из вложенных циклов.
 |
 |
Рис. 35. Алгоритм ввода элементов двумерного массива
При рассмотрении в дальнейшем алгоритмов обработки элементов двумерного массива в целях сокращения их размера фрагмент ввода элементов будем заменять отдельным блоком ввода.
Пример 13. Составить алгоритм поиска максимального значения в двумерном массиве А(N,M).
 |
Решение. Поиск максимального элемента в двумерном массиве осуществляется аналогично поиску в одномерном массиве. Отличие состоит в том, что для обработки двумерного массива используем влож Обозначим максимальный элемент переменной МАХ.
Значение этой переменной будет меняться на каждой итерации цикла, если очередной значение элемента массива окажется больше МАХ (см. рис.36).
Рис.36. Алгоритм поиска максимального значения в двумерном массиве
Пример 14.Составить алгоритм вычисления количества нечетных элементов в каждой строке двумерного массива А(1.. N, 1..М).
 |
 |
 |
 |
 |
Решение.
Алгоритм представлен на рисунке 17. В этом алгоритме переменная К - является счетчиком элементов массива, S - сумма элементов массива, она вычисляется по реккурентной формуле S=S+A(K).
Ввод количества и значений элементов массива осуществляется вначале в отдельном блоке ввода, который реализуется по
схеме алгоритма ввода элементов массива, изображенного на рис.16.
Часто для проверки правильности работы алгоритмов на конкретных наборах данных используют таблицу трассировки. Эта таблица содержит столько столбцов, сколько переменных и условий в алгоритме, в ней мы выполняем действия шаг за шагом от начала до конца алгоритма для конкретных наборов входных данных.
Пример 10. Составить алгоритм поиска элемента с максимальным значением в
одномерном массиве А(1..n) и его таблицу трассировки для значений (3, 7, 0, 9).
Решение.
Введем обозначения K- текущий номер элемента, A[K] - текущее значение элемента массива, N=4 количество элементов одномерного массива, M- номер максимального элемента массива, A[M] - значение максимального элемента массива. Основной идеей алгоритма является выполнение сравнения текущего элемента массива A[K] и элемента с максимальным значением A[М],
 |
определенным на предыдущем шаге итерации. По алгоритму изображенному на рис.18 получено максимальное значение для массива (3, 7, 0, 9), процесс и правильный результат поиска которого показаны в таблице 4.
Рис.18. Алгоритм поиска максимального значения в массиве
Таблица 4. Таблица трассировки алгоритма примера 10.
|
Номер элемента массива К |
Значение элемента А (К) |
Номер максимального М |
Значение максимальнго А(М) |
Проверка А(К)>А(М) |
||
|
1 |
3 |
1 |
3 |
Нет |
||
|
2 |
7 |
1 |
2 |
3 |
7 |
да |
|
3 |
0 |
2 |
7 |
нет |
||
|
4 |
9 |
2 |
4 |
7 |
9 |
да |
Если очередной элемент равен 0, то для подсчета количества таких элементов используем реккурентную формулу M=M+1. В тот момент времени, когда значение М=2, нам необходимо запомнить номер текущего элемента массива, так как это и есть искомый второй положительный элемент исходного массива. На рис.20 приведен фрагмент алгоритма, реализующего поиск второго нулевого элемента в некотором массиве А из N элементов.
Рис. 20. Фрагмент алгоритма поиска второго нулевого элемента в массиве А, состоящем из N элементов. Здесь К- номер очередного элемента, А(К) - значение очередного элемента, m -количество нулевых элементов, Р- номер второго нулевого элемента в массиве
 |
Поиск последнего положительного элемента массива будем осуществлять аналогично в цикле, запоминая номер очередного элемента, значение которого больше нуля, в дополнительной переменной S. Учитывая тот факт, что после того, как будут просмотрены и проверены на положительность все элементы массива, в переменной S будет храниться номер последнего положительного элемента массива. На рис. 21 представлен фрагмент алгоритма поиска последнего положительного элемента в массиве А.
 |
Рассмотрим фрагменты алгоритма, приведенные на рис. 20 и 21. Можно заметить, что оба этих фрагмента выполняют поиск под управлением цикла, с одинаковым числом повторений, равным количеству элементов исходного массива N. Поэтому в итоговом алгоритме решения задачи примера 11 вместо композиции этих двух фрагментов в виде двух последовательных циклов можно использовать параллельное выполнение операций поиска под управлением одного цикла, который приведен на рис. 22.
 |
Напомним, что исходный одномерный массив содержит 9 элементов: (5, 0, 4, -3, -7, 0, -2, -4, 0).По условию задачи необходимо поменять местами 2-ой нулевой элемент и последний положительный элемент.
Так как задачи поиска необходимых для перестановки элементов алгоритмически решены (рис. 22), то рассмотрим задачу перестановки элементов.Для реализации перестановки найденных элементов достаточно воспользоваться управляющей структурой следования. Для того, чтобы во время перестановки не потерять переставляемые значения используем дополнительную переменную Q, временно хранящую одно из переставляемых значений элемента массива, в частности, второе нулевое значение.На рис. 23 представлен универсальный алгоритм перестановки двух элементов одномерного массива, имеющих порядковые номера P и S .
 |
Рис. 23.Фрагмент перестановки двух элементов массива, с номерами S и P
 |
Рис. 24. Алгоритм вывода элементов массива
 |
Таким образом, процесс проектирование первоначального алгоритма перестановки второго нулевого элемента и последнего положительного элемента в одномерном массиве завершен. Полученный алгоритм представлен на рис.25. Следует заметить, что целью решения примера 11 было показать процесс нисходящего проектирования алгоритма " сверху-вниз " с использованием декомпозиции и метода структурной алгоритмизации. Отметим, что с целью упрощения в полученном алгоритме не рассматриваются ситуации, когда в составе элементов массива отсутствуют положительные значения или нулевые значения в количестве большем одного.
 |
|||
 |
|||
 |
Для проверки правильности работы полученного алгоритма составим таблицу трассировки для одномерного массива из 9 элементов: (5, 0, 4, -3, -7, 0, -2, -4, 0), приведенных в примере 11.
Напомним, что заполнение таблицы происходит по строкам. Считаем, что все начальные значения числовых переменных равны 0.
В таблице 5 выполнена трассировка фрагмента поиска второго нулевого и последнего положительного элементов (их номеров), а в таблице 6 выполнена трассировка следующего фрагмента алгоритма по перестановке в массиве найденных элементов, где K- текущий номер элемента, A[K] - текущее значение элемента массива, М- количество нулей, обнаруженных в массиве при анализе очередного элемента, P- номер второго нулевого элемента массива, S- номер последнего положительного элемента массива, A[S] - значение последнего положительного элемента массива, A[P] - значение второго нулевого элемента массива.
Таблица 5.Таблица трассировки операций Таблица 6. Таблица трассировки
поиска второго нулевого элемента и перестановки найденных элемен-
последнего положительного тов массива
|
К |
Входной массив А(К) |
M |
М=2 |
Р |
S |
A(P) А(6) |
Q |
А(S) А(3) |
Выходной массив А(К) |
|
|
1 |
5 |
0 |
Нет |
1 |
0 |
0 |
4 |
1 |
5 |
|
|
2 |
0 |
1 |
Нет |
4 |
0 |
4 |
2 |
0 |
||
|
3 |
4 |
3 |
4 |
0 |
0 |
3 |
0 |
|||
|
4 |
-3 |
4 |
-3 |
|||||||
|
5 |
-7 |
5 |
-7 |
|||||||
|
6 |
0 |
2 |
Да |
6 |
6 |
4 |
||||
|
7 |
-2 |
7 |
-2 |
|||||||
|
8 |
-4 |
8 |
-4 |
|||||||
|
9 |
0 |
3 |
Нет |
9 |
0 |
Решение. Анализ постановки задачи позволяет выделить две последовательно решаемые задачи: поиск элемента с максимальным значением и удаление этого значения из массива.
Алгоритм первой задачи был рассмотрен ранее в примере 10 (рис.18). В этом алгоритме был определен номер максимального значения М, а максимальное значение определялось как А(М). Удаление элемента из массива приводит к уменьшению количества элементов массива за счет их перемещения на позицию удаляемого. Например, требуется удалить максимальное значение в массиве (2,4,13,5,7). Максимальное значение в этом примере равно 13. После удаления количество элементов данного массива уменьшится на 1 и станет равным 4, а массив примет вид (2,4,5,7). Таким образом, можно сделать вывод , что для удаления элемента из массива необходимо знать его номер, например М, удаление производится путем сдвига на одну позицию влево всех следующих за удаляемым элементов А(М)=А(М+1), этот сдвиг должен осуществляться под управлением цикла. Цикл завершит свою работу, когда последний элемент массива сдвинется на место предпоследнего элемента .
После приведенных рассуждений и используя алгоритмическое решение примера 10, изображенное на рис.18, составим алгоритм удаления элемента с максимальным значением из одномерного массива из N элементов (см. рис.26).
 |
К - номер очередного элемента, М- номер элемента с максимальным значением, N-1 - уменьшенное в результате удаления одного элемента количество элементов массива А, A [K]: =A [K+1] - удаление путем сдвига влево следующих за удаляемым элементов на одну позицию.
Алгоритмы обработки одномерных символьных массивов
Одномерные символьные масивы
- это массивы, составленные из определенной последовательности символов, которые образуют тексты. Основными операциями, выполняемыми над текстами, являются операции по определению слов, выделению слова с максимальной длиной, удаление и перестановка слов,сортировка по алфавиту идр.
Для простоты будем считать, что символьный массив представляет одну строку произвольного текста, слово - любую последовательность подряд идущих символов не содержащую пробела. Пробел - это специальный символ, используемый для отделения слов, он не может располагаться перед первым словом. Учитывая все эти допущения можно предложить для решения задачи определения количества слов использовать подсчет количества элементов массива, равных пробелу минус 1.
Рассмотрим алгоритмическое решение распространенной задачи определения в массиве символов слова с максимальной длиной.
Пусть исходный массив А содержит N символов. Для определения слова с максимальной длиной будем использовать сравнение длины текущего слова М с длиной предыдущего слова МАХ. Длина слова определяется как содержащееся в нем количество символов. Для того, чтобы вывести слово с максимальной длиной, необходимо запомнить номер элемента S, с которого начинается это слово.
Алгоритм поиска в символьном массиве слова с максимальной длиной приведен на рис. 32, а его таблица трассировки для массива (Дул теплый ветер)- в таблице 8.
 |
Рис. 32.Алгоритм поиска в символьном массиве слова с максимальной длиной
Таблица 8. Таблица трассировки алгоритма поиска слова с максимальной длиной при N= 16 в тексте : "Дул теплый ветер"
| К | А(К) | К=N | А(К)=" " | М>МАХ | М | МАХ | S | НОВОЕ S | |||||||||
| 1 | Д | Нет | Нет | 1 | 0 | 1 | 1 | ||||||||||
| 2 | у | Нет | Нет | 2 | |||||||||||||
| 3 | л | Нет | Нет | 3 | |||||||||||||
| 4 | " " | Нет | ДА | Да | 0 | 3 | 3 | 4 | |||||||||
| 5 | т | Нет | Нет | 1 | |||||||||||||
| 6 | е | Нет | Нет | 2 | |||||||||||||
| 7 | п | Нет | Нет | 3 | |||||||||||||
| 8 | л | Нет | Нет | 4 | |||||||||||||
| 9 | ы | Нет | Нет | 5 | |||||||||||||
| 10 | й | Нет | Нет | 6 | |||||||||||||
| 11 | " " | Нет | ДА | Да | 0 | 6 | 10 | 11 | |||||||||
| 12 | в | Нет | Нет | 1 | |||||||||||||
| 13 | е | Нет | Нет | 2 | |||||||||||||
| 14 | т | Нет | Нет | 3 | |||||||||||||
| 15 | е | Нет | Нет | 4 | |||||||||||||
| 16 | р | Да | Нет | Нет | 5 |
/p>
Рассмотрите результат, приведенный в таблице 8, для конкретного входного символьного массива "Дул теплый ветер" без последнего столбца. Однако, после выполнения приведенного на рис. 32 алгоритма для предложения "Дул теплый ветер" будет выведено слово из 7 символов, начинающихся с пробела :" теплый". Значит, формулу определения номера символа S = K-1 , с которого начинается слово с максимальной длиной, следует изменить на S = K. При этом надо будет изменить содержание блока вывода результата: вместо A( S -MАХ), … A(S) следует использовать A( S -MАХ), … A(S-1). Таким образом, таблица трассировки показала наличие ошибок в алгоритме, изображенном на рис. 32. После внесения изменений этот алгоритм будет работать правильно (см. модернизированный алгоритм поиска в символьном массиве слова с максимальной длиной на рис. 33).
 |
Алгоритмы обработки последовательностей чисел
Последовательность значений - это набор однотипных величин, которые вводятся и обрабатываются циклически. Примером последовательности целых чисел может быть следующий набор значений: (2,5,-4,10,1,0). Последовательности значений отличаются от массивов значений тем, что в памяти одновременно все значения последовательности не хранятся. Для обозначения значения последовательности используют одну переменную, в которую на каждом шаге итерации вводится очередное значение последовательности. Отличительной особенностью последовательности является также возможность содержания неопределенного или неизвестного заранее количества ее значений. В этом случае критерием окончания последовательности служит некоторое особое значение, например, ноль.
Пример 7. В числовой последовательности определить сумму положительных и произведение отрицательных чисел. Решение представить с использованием циклического алгоритма с предусловием. Признак конца последовательности - значение 0.
Решение.
Обозначим за Х переменную, содержащую очередное значение последовательности, за S - сумму положительных значений , за Р - произведение отрицательных значений. Полученный алгоритм приведен на рис. 14. Условие
 |
Рис.14. Алгоритм вычисления суммы положительных и произведения отрицательных значений числовой последовательности
для выбора вычислений Х>0. Для вычисления суммы значений воспользуемся реккурентной формулой S=S+X с начальным значением S=0, для вычисления произведения - реккурентной формулой P=P*X с начальным значением Р=1. Условие выхода из цикла неравенство Х<>0.
Пример 8.Составить циклический алгоритм с постусловием для определения в последовательности целых чисел количества четных чисел.
 |
Решение. Обозначим за Х переменную, содержащую очередное значение последовательности, за K - количество четных значений (рис. 15). Условие для выбора четных значений Х mod 2=0 (остаток при делении Х на 2 равен 0). Для вычисления количества значений воспользуемся реккурентной формулой К=К+1 с начальным значением К=0.
 |
|||||
 |
 |
||||
Алгоритмы обработки упорядоченных массивов
Рассмотренные выше алгоритмы сортировки считаются одними из важнейших процедур упорядочивания структурированной данных, хранимых в виде массивов. Одной из главных целей задач сортировки массивов является облегчение их дальнейшей обработки, так как для упорядоченных данных разработаны эффективные методы поиска и обновления. Так, например, поиск минимального или максимального значения в упорядоченном массиве сводится к выборке первого или последнего элемента массива. Рассмотрим некоторые алгоритмы обработки упорядоченных массивов.
Алгоритмы сортировки одномерных массивов
Под сортировкой понимают процесс перестановки объектов данного массива в определенном порядке. Целью сортировки являются упорядочение массивов для облегчения последующего поиска элементов в данном массиве. Рассмотрим основные алгоритмы сортировки по возрастанию числовых значений элементов массивов. Существует много методов сортировки массивов. В этой работе будут рассмотрены алгоритмы двух методов: модифицированного метода простого выбора и метода парных перестановок.
Анализ постановки задачи и ее предметной области
На первом этапе уточняется постановка задачи, после чего выявляются отдельные явления, объекты, процессы, их связи и зависимости предметной области.
Здесь определяются такие понятия как исходные и результирующие данные, абстрактно представляющие информацию о процессах предметной области реального мира, а также поясняются каким образом из исходных данных могут быть получены результирующие.
Исходные данные должны быть полными, т.е. содержать данные, необходимые и достаточные для решения задачи. Если данные неполные, необходимо приложить дополнительные усилия для сбора дополнительных сведений; эта ситуация может также возникнуть на последующих этапах при выборе метода решения.
Различают исходные данные трех видов: постоянные, условно-постоянные и переменные.
Постоянные исходные данные - это данные, которые сохраняют свои значения в процессе решения задачи (математические константы, координаты неподвижных объектов) и не зависят от внешних факторов.
Условно-постоянные данные - это данные, которые могут иногда изменять свои значения; причем эти изменения не зависят от процесса решения задачи, а определяются внешними факторами (величина подоходного налога, курс валют, количество дней в году).
Переменные данные - это данные, которые изменяют свои значения в процессе решения задачи.
На этом этапе важно не только классифицировать данные по отношению к процессу решения, но определить их наименование, тип, структуру и ограничения, накладываемые на значения. Желательно также определить допустимые и недопустимые операции по отношению к различным типам исходных данных.
Классификация данных по структурному признаку

Нечисловые Числовые Однородные Неоднородные
Рис. 1. Классификация данных
На рис.1 представлена классификация данных.
Данное относят к простому типу, если в любой момент времени оно определяет одно и только одно значение.
Диапазон изменения возможных значений определяется типом данных. Например, требуется вычислить площадь поверхности некоторого тела. Очевидно, что для представления информации о вычисляемой площади поверхности некоторого тела достаточно использовать данное простого числового типа. Простые данные определяют такое отношение: одно имя - одно значение.
Структурированные данные отличаются от простых тем, что к ним применимо другое отношение: одно имя - много значений. Если все элементы, входящие в такую структуру, однотипны, то такая структура называется однородной, в противном случае - неоднородной. Классическим примером однородной структуры является массив, являющийся последовательностью однотипных значений, таких как, например, (2,51,3,7,88). Неоднородная структура в отличие от однородной содержит значения различных типов, относящихся к одному понятию или объекту, и, значит, такое структурированное данное несет в себе больше информации. Для представления неоднородных структур используют запись. Запись - это структура, предназначенная для представления данных различного типа. Запись состоит из поименованных полей, каждое из которых должно содержать значение определенного типа.
Рассмотрим простой пример. Задача заключается в определении в некоторой стране города с максимальным количеством жителей. Данные, которые необходимо проанализировать, это нечисловые данные, содержащие информацию о названии города, и числовые данные, содержащие информацию о численности населения в этом городе. В качестве структуры, содержащей данные о названии города и количестве в нем жителей, следует выбрать неоднородную структуру - запись, пример которой изображен в таблице 1.
Таблица 1.Пример записи
|
Имя поля: Город |
Имя поля: Количество жителей |
|
Тип поля: Строка символов |
Тип поля: Число |
|
Значение: Москва |
Значение: 8 578 676 |
Определение отношений между данными, условий и ограничений, накладываемых на значения данных и эти отношения, зависит от конкретной постановки задачи и требований пользователя.
В результате анализа постановка и требования задачи могут быть представлены в обобщенном виде.
Циклические алгоритмы
Циклические алгоритмы
являются наиболее распространенным видом алгоритмов, в них предусматривается повторное выполнение определенного набора действий при выполнении некоторого условия. Такое повторное выполнение часто называют циклом.
Существуют два основных видов циклических алгоритмов: циклические алгоритмы с предусловием, циклические алгоритмы с постусловием. Они отличаются друг от друга местоположением условия выхода их цикла.
Цикл с предусловием
начинается с проверки условия выхода из цикла. Это логическое выражение, например I<=6. Если оно истинно, то выполняются те действия, которые должны повторяться. В противном случае, если логическое выражение I<=6 ложно, то этот цикл прекращает свои действия.
Цикл с постусловием функционирует иначе. Сначала выполняется один раз те действия, которые подлежат повторению, затем проверяется логическое выражение , определяющее условие выхода из цикла, например, I>6 .Проверка его осуществляется тоже по-другому. Если условие выхода истинно, то цикл с постусловием прекращает свою работу, в противном случае - происходит повторение действий, указанных в цикле. Повторяющиеся действия в цикле
 |
называются "телом цикла". Разновидности циклов приведены на рис. 10а),б).
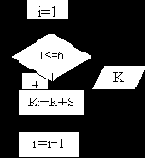 |
| а) Цикл с постусловием б) Цикл с предусловием
Рис. 10. Виды циклических алгоритмов Классическим примером циклического алгоритма служит алгоритм для вычисления степени числа Y=X? . Этот алгоритм может быть реализован на основе операции умножения. Табличное представление такого алгоритма, отражающего зависимость У от Х при изменении показателя степени n от 1 до 3, представлено в табл.3. В этой таблице показанны также реккурентные соотношения между У и Х, определяющие как на каждом шаге зависит значение У от значения Х и от значения У, вычисленного на предыдущем шаге. Таблица 3.Реккурентные соотношения при вычислении Y=X? |
||||||
|
n |
Y |
Реккурентные соотношения |
||||
|
|
||||||
|
1 |
Y[1]=X |
Y=X |
||||
|
2 |
Y[2]=X*X или Y[2]=Y[1]*X |
Y=X*X или Y=Y*X |
||||
|
3 |
Y[3]=X*X*X или Y[3]=Y[2]*X |
Y=X*X*X или Y=Y*X |
||||
Пример 5. Пусть требуется составить алгоритм вычисления суммы ряда S=x+x^2+x^3+…+x^n. Решение. Исходные данные для алгоритма это переменные x и n. На каждом шаге будем вычислять очередной член суммы Y и прибавлять его к предыдущему значению суммы S.Для этого используем реккурентную формулу вычисления степени Х (см. таблицу 3) Y=Y*Х, тогда сумма ряда на каждом шаге итерации будет вычисляться по формуле S=S+Y. Количество итераций K изменяется от 1 до n и равно количеству членов ряда. Начальное значение суммы ряда S равно 0. На рис. 12 представлен циклический алгоритм с предусловием для вычисления заданной суммы ряда. Пример 6. Требуется составить алгоритм получения на отрезке [-15,15] множества значений функции Y= SIN(X) в виде таблицы значений (X,Y) при изменении аргумента Х по формуле X[k]=X[k-1]+h, где h=1,5. Решение. Такие задачи относят к задачам табулирования функций. Из
|
||||||
Формальное решение задачи
После проведения анализа постановки задачи, выявления данных, их структуры и отношений между ними можно приступить к построению формальной модели. Это наиболее важный этап в процессе решения задачи.
Модель - это упрощенное представление о реальном объекте, процессе или явлении. Моделирование - построение моделей для исследования и изучения моделируемого объекта, процесса, явления с целью получения новой информации при решении конкретных задач.
Для описания модели предметной области решаемой задачи необходимо выбрать некоторую формальную систему. Обычно, исходя из постановки задачи, можно сразу определить один или несколько видов моделей, подходящих для описания и моделирования решения вашей задачи: математические, геометрические, структурные, логические и др.
Наиболее распространенными и хорошо изученными являются математические модели, описывающие зависимости между данными числового типа. Например, в качестве математической модели звезды можно использовать систему уравнений, описывающих процессы, происходящие в недрах звезды. Математической моделью другого рода являются математические соотношения, позволяющие рассчитать оптимальный план работы предприятия. К основным достоинствам математических моделей безусловно относятся хорошо изученные и широко применяемые математические методы решения большого класса задач, что значительно облегчает формирование основной идеи и выбор методов решения задачи.
Приступая к разработке модели, следует попытаться решить задачу для конкретных входных данных, затем обобщить полученное решение на основе его анализа для любых значений входных данных. Перед тем как определить решение задачи для конкретных входных данных целесообразно найти ответ на следующие вопросы:
Существуют ли решения аналогичных задач?
Какая математическая модель больше всего подходит для решения этой задачи?
Пример 1.Постановка задачи. Требуется определить пригодность данной аудитории для проведения учебных занятий.
Решение.
Этап 1.
Анализ постановки задачи и ее предметной области.
В результате анализа предметной области, выявляем, что эта предметная область связана с образовательным процессом. И постановка задачи может быть переформулирована следующим образом. Определить, подходит ли некоторая аудитория для проведения занятий группы учеников при некоторой норме площади для каждого ученика. Введем обозначения для входных и выходных данных. Исходные данные должны быть представлены простыми переменными значениями числового типа: А - ширина аудитории, B - ее длина, К - количество учеников в группе, N - допустимое минимальное количество квадратных метров для одного ученика (норма ), M - количество парт в аудитории. В качестве выходных данных будут выступать сообщения: " Аудитория может быть использована для поведения учебных занятий " и " Аудитория не может быть использована для поведения учебных занятий ".
Этап 2. Формальное решение.
Определим отношения между входными и выходными данными. Для этого введем промежуточные данные числового типа : S - площадь аудитории, C - требуемая по нормам площадь для проведения занятий для группы из К учеников, D - требуемое количество парт для обучения группы, состоящей из К учеников. Опишем соотношения между входными и выходными данными, используя математические зависимости. Математическая модель:
S = A*B,
C=N*K, S>=C, K<=2*D.
Литература
1. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов: Пер. с англ.-М.: Мир,1979.
2. Ван Тассел Д. Стиль, разработка, эффективность, отладка и испытание программ.- М.: Мир, 1981.
3. Вирт Н. Алгоритмы и структуры данных.- М.Мир,1989.
4. Гейн А.Г. и др. Основы информатики и вычислительной техники.- М.Просвещение , 1992.
5. Гудман С., Хидетниели С. Введение в разработку и аналих алгоритмов. - М.: Мир, 1981.
6. Дайтибегов Д.М., Черноусов Е.А. Основы алгоритмизации и алгоритмические языки.- М.: Финансы и статистика, 1992.
7. Коллинз Г. Блэй Дж. Структурные методы разработки систем: от стратегического планирования до тестирования.Пер. с англ./ Под ред. В.М. Савинкова.- М.:Финансы и статистика, 1986.
8. Кузнецов А.А. и др. Основы информатики.- М.:Дрофа, 1998.
9. Кушниренко А.Г. и др. Информатика.- М.:Дрофа, 1998.
10. Ландо С.К. Алгоритмика: Методическое пособие. - М.: Дро фа,1997.
11. Марков А.А., Нагорный Н.М. Теория алгорифмов.-М.:Наука. Главная редакция физико-математической литературы, 1984.
12. Матросов В.Л. Теория алгоритмов. - М.: Прометей, 1989.
13. Могилев и др. Информатика: Учебное пособие для вузов / А.В.Могилев,Н.И.Пак, Е.К.Хеннер; Под ред. Е.К. Хеннера. - М.: Изд. центр "Академия", 2000.
14. Светозарова Г.Н. и др. Практикум по программированию на языке Бэйсик.- М.:Наука, 1988.
15. Успенский В.А., Семенов А.Л. Теория алгоритмов: основные открытия и приложения.- М.: Наука, 1987.
16. Хохлюк В.И. Параллельные алгоритмы целочисленной оптимиза ции.-М.: Радио и связь,1987.
Основные средства представления алгоритмов
Алгоритм моделирует решение задачи в виде точно определенной последовательности действий для некоторого исполнителя по преобразованию исходных данных в результирующие. Процесс составления алгоритмов называют алгоритмизацией.
Алгоритм, реализующий решение задачи, можно представить различными способами: с помощью графического или текстового
описания, в виде таблицы значений. Графический способ представления алгоритмов имеет ряд преимуществ благодаря визуальности и явному отображению процесса решения задачи. Алгоритмы, представленные графическими средствами, получили название визуальные алгоритмы. Текстовое описание алгоритма является достаточно компактным и может быть реализовано на абстрактном или реальном языке программирования в виде программы для ЭВМ. Таблицы значений представляют алгоритм неявно, как некоторое преобразование конкретных исходных данных в выходные. Табличный способ описания алгоритмов может быть с успехом применен для проверки правильности функционирования разработанного алгоритма на конкретных тестовых наборах входных данных, которые вместе с результатами выполнения алгоритма фиксируются в "таблицах трассировки".
Таким образом, все три способа представления алгоритмов можно считать взаимодополняющими друг друга. На этапе проектирования алгоритмов наилучшим способом является графическое представление, на этапе проверки алгоритма - табличное описание, на этапе применения - текстовая запись в виде программы.
Основы алгоритмизации
Слово «алгоритм» появилось в 9-м веке и связано с именем математика Аль-Хорезми, который сформулировал правила выполнения четырех арифметических действий над многозначными числами.
В настоящее время понятие алгоритма - одно из фундаментальных понятий науки информатика. С одной стороны алгоритм является предметом изучения такой отрасли математики как теория алгоритмов (Марков [1]), с другой стороны в информатике существует неформальное определение алгоритма, и алгоритмизация выступает в качестве общего метода информатики.
Объектом приложения алгоритмов являются самые различные науки и области практической деятельности (Хохлюк[3],Ахо [2]). Широкое применение алгоритмов для решения практических задач не только при использовании ЭВМ позволяет рассматривать эту область информатики как отдельную дисциплину - алгоритмику.
Алгоритм – это точно определенная последовательность действий для некоторого исполнителя, выполняемых по строго определенным правилам и приводящих через некоторое количество шагов к решению задачи.
Исполнитель алгоритмов
определяет элементарные действия, из которых формируется алгоритм. Отдельные действия, составляющие алгоритм, называются операциями. При этом под операцией понимается как какое-то единичное действие, например, сложение, так и группа взаимосвязанных действий.
Основными особенностями любого алгоритма являются решение задачи в обобщенном виде и возможность выполнять действия по решению задачи для конкретных значений (не только человеку, но и различным техническим устройствам (исполнителям)). Основным исполнителем несложных алгоритмов является человек. Достаточно вспомнить последовательность действий для решения систем линейных уравнений, вычисления корней уравнений.
При решении сложных задач исполнителем является ЭВМ и составление алгоритма решения задачи является необходимым этапом, детализирующим метод решения для дальнейшего программирования. Программа осуществляет еще более глубокую детализацию решения и его визуализацию.
Свойства алгоритма:
Определенность – выполнив очередное действие, исполнитель должен точно знать, что ему делать дальше.
Дискретность – прежде, чем выполнить определенное действие, надо выполнить предыдущее.
Массовость – по одному и тому же алгоритму решаются однотипные задачи и неоднократно.
Понятность – алгоритм строится для конкретного исполнителя человеком и должен быть ему понятен. Это облегчает его проверку и модификацию при необходимости .
Результативность – алгоритм всегда должен приводить к результату.
Можно сказать, что в процессе формального решения задачи, ее решение сначала описывается на языке математики в виде системы формул, а затем на языке алгоритмов в виде некоторого процесса, в котором используются ранее определенные математические формулы и условия их выполнения. Таким образом, алгоритм может рассматриваться как связующее звено в цепочке "метод решения - реализующая программа".
Ответы и решения
Ответы к теме разветвленные алгоритмы
Задача 7

Ответы к теме циклические алгоритмы
 |
Задача 6.
Ответы к теме циклические алгоритмы
Задача 12.
 |
Ответы к теме одномерные массивы
Задача 1.
 |
Ответы к теме одномерные массивы
Задача 10.
 |
 |
Ответы к теме одномерные массивы
Задача 13.
 |
Учебное издание
АФАНАСЬЕВАТатьяна Васильевна.
Основы визуальной алгоритмизации
Учебное пособие
Редактор Н.А. Евдокимова.
Изд.лиц.020640 от 22.10.97
Подписано в печать . Формат 60 Х 84 /16. Бумага писчая.
Усл. печ. л. 4,19 . Уч.-изд.л.4,29 . Тираж 300 экз.
Заказ
Ульяновский государственный технический университет
432027, Ульяновск, Сев. Венец,32.
Типография УлГТУ, 432027, Ульяновск, Сев. Венец,32.
Поиск элементов в упорядоченном массиве
Задача поиска значения Х в упорядоченном по возрастанию значений массиве A(1)<A(2)<,..,<A(n) формулируется следующим образом. Требуется выяснить входит ли значение Х в этот упорядоченный массив, и если входит, то определить значение k, для которого А(k)=Х. Для такого типа задач применяется эффективный метод бинарного поиска, который также известен, как метод деления пополам. Сущность этого метода поиска заключается в последовательном определении номера S элемента, расположенного в точке деления упорядоченного массива пополам и сравнении искомого значения Х с этим элементом массива A(s). Если A(s)=Х, то поиск заканчивается. В противном случае возможны две ситуации: если A(s)<Х, то все элементы, имеющие номера с 1 по s также меньше Х, если A(s)>Х, то все элементы, имеющие номера с S по n также больше Х в силу упорядоченности массива по возрастанию значений. Поэтому для дальнейшего поиска половину значений массива можно исключить из рассмотрения. В первом случае - левую, во втором случае - правую половину. Рассмотрим пример. Допустим, что требуется определить совпадает ли значение Х=12 с каким-либо элементом в упорядоченном массиве А и если совпадает, то определить порядковый номер S этого элемента. Иллюстрация применения метода бинарного поиска для поиска элемента Х=12 в массиве (2,3,4,6,10,12,20,30,35,45) приведена на рис. 30.
Элементы массива А (2,3,4,6,10,12,20,30,35,45).
Номера элементов 1 2 3 4 5 6 7 8 9 10.
Первое деление S=5, А(5)=10 А(5)<Х), исключаем левую половину.
Элементы массива А (2,3,4,6,10,12,20,30,35,45).
Номера элементов 1 2 3 4 5 6 7 8 9 10.
Второе деление S=8, А(8)=30 А(8)>Х), исключаем правую половину.
Элементы массива А (2,3,4,6,10,12,20,30,35,45).
Номера элементов 1 2 3 4 5 6 7 8 9 10.
Третье деление S=6, А(6)=12 А(6)=Х), элемент Х=12 найден.
Рис.30. Иллюстрация применения метода бинарного поиска
 |
На рис.31 представлен алгоритм, реализующий метод бинарного поиска в упорядоченном массиве.
Рис.31.Алгоритм поиска методом бинарного поиска
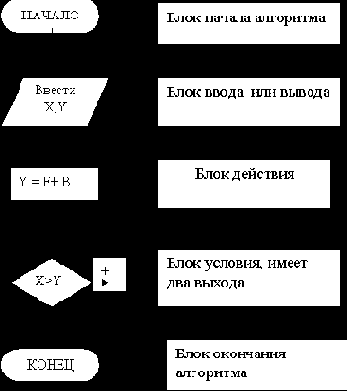
таблица соответствия алгоритмических и программных фрагментов
| Фрагменты блок-схем алгоритмов |
Назначение | Соответствующие фрагменты программ
на языке Паскаль | ||||||||||||
 |
Начало и конец алгоритма | Begin
End | ||||||||||||
|
Блок обработки, в нем вычисляются новые значения или производится вызов подпрограммы. |
X: =A+B | ||||||||||||

x ">
|
Ввод исходных данных или вывод результатов. |
Read (x, y) Write (x, y) | ||||||||||||
 
_ _
+ | Ветвление полное.
Если значение переменной a больше b, то выполняется x=a , иначе x=b. |
If a>b then X: =a else X:=b
| ||||||||||||
  
_ _ _
+ | Ветвление неполное.
Если значение переменной a больше b, то выполняется x=a. | If a>b then x:=a | ||||||||||||
 
_ + +
| Цикл с предусловием. Пока значение условия i<6 истино выполняется тело цикла, то есть действия К=К+1 и i=i+2. Переменная i определяет количество повторений и называется счетчиком цикла. |
i: =1; While i<6 do Begin K: =K+1; i: =i+2; End; Write(K);
| ||||||||||||
- + _ + | Цикл с постусловием.
Пока значение условия i>6 ложно выполняется тело цикла, то есть действия К=К+1 и i=i+0,1.Переменная i определяет количество повторений в цикле и называется счетчиком цикла. |
i: =1; Repeat K: =K+1; i: =I+0.1; Until I>6; Write(K); |
||||||||||||
  
  
+ |
Цикл с постоянным приращением счетчика. В этом цикле изменение счетчика цикла i происходит только на единицу. Пока значение счетчика цикла меньше или равно 6 Выполняется тело цикла, то есть действия K=K+S и i=i+1. |
For i: =1 to 6 do K: =K+S; Write(K); |
тестовый самоконтроль
1. При исходных данных А: = 5, В: = 4 определите результат выполнения визуального алгоритма, изображенного ниже. Определите из каких структурных фрагментов состоит он и к какому виду он относится.
1) 
2) Х = 9
3) 
4) 
 |

![]()

![]()

![]()

|
|

![]()

![]()

2. Алгоритм закончит работу при начальных значениях
1) А = 0; С = 1
2) 
 для определения элементов выше главной диагонали достаточно использовать условие I<J, ниже главной диагонали I>J. По условию задачи нам требуется найти сумму элементов двумерного массива А(1.. N, 1..М), расположенных выше главной диагонали, значит применим условие I<J, связывающее такие параметры элемента массива как номер строки I и номер столбца J.
для определения элементов выше главной диагонали достаточно использовать условие I<J, ниже главной диагонали I>J. По условию задачи нам требуется найти сумму элементов двумерного массива А(1.. N, 1..М), расположенных выше главной диагонали, значит применим условие I<J, связывающее такие параметры элемента массива как номер строки I и номер столбца J. Данный алгоритм содержит два вложенных цикла, каждый из которых относится к циклу с постусловием.
Данный алгоритм содержит два вложенных цикла, каждый из которых относится к циклу с постусловием.  переменной К, которая называется счетчиком элементов массива А (рис.16), эта же переменная К определяет количество итераций циклического алгоритма ввода элементов массива. На каждом шаге итерации переменная К(значение номера элемента массива А) изменяется на 1, то есть происходит переход к новому элементу массива.В дальнейшем, при рассмотрении алгоритмов обработки одномерных массивов в целях устранения дублирования алгоритм ввода элементов массива будем заменять одним блоком, подразумевая, что он реализуется по схеме, циклического алгоритма, представленного на ри- сунке 16.
переменной К, которая называется счетчиком элементов массива А (рис.16), эта же переменная К определяет количество итераций циклического алгоритма ввода элементов массива. На каждом шаге итерации переменная К(значение номера элемента массива А) изменяется на 1, то есть происходит переход к новому элементу массива.В дальнейшем, при рассмотрении алгоритмов обработки одномерных массивов в целях устранения дублирования алгоритм ввода элементов массива будем заменять одним блоком, подразумевая, что он реализуется по схеме, циклического алгоритма, представленного на ри- сунке 16. Пример 9. Составить алгоритм определения в одномерном числовом массиве А из N элементов суммы положительных элементов.
Пример 9. Составить алгоритм определения в одномерном числовом массиве А из N элементов суммы положительных элементов.