Алгоритм

ОПЕРАЦИИ НАД СТЕКАМИ:

- PUSH ( s , i ) - занесение элемента в стек, где s - название стека, i - элемент, который заносится в стек;

- POP ( s ) - выборка элемента из стека. При выборке элемент помещается в рабочую область памяти, где он используется;

- EMPTY ( s ) - проверка стека на пустоту (true - пуст, false - не пуст);

- STACKTOP ( s ) - чтение верхнего элемента без его удаления.

Фрагмент программы создания стека (необходимые процедуры)

Program STACK;

  const

     max_st=50;

const

    max_st=50;

  var

    st,st2: array[1..max_st] of integer;

    n:integer;

  function empty:boolean;  {Проверка стека на наличие элементов в нем}

    begin

        empty:=n=0

    end;

  procedure push(a:char);  {Поместить элемент в стек}

    begin

      inc(n);

      st[n]:=a;

    end;

  procedure pop(var a:char);  {Извлечь элемент из стека}

    begin

      a:=st[n];

      dec(n);

    end;

  function full:boolean;   {Проверка на переполнение}

    begin

      Full:=n=max_st

    end;

  procedure stacktop(var a:char);  {Узнать верхний элемент}

    begin

      a:=st[n];

    end;

  begin  {Основная программа}

     .

     .

end.

Алгоритм

 

Операции с односвязными списками.

1.   Вставка элемента в начало односвязного списка.

Вставим в начало данного списка элемент, информационное поле которого содержит переменную D. Чтобы это осуществить, необходимо произвести следующие действия :

а) Создать пустой элемент, на который указывает указатель p.

b) Информационному полю созданного элемента присвоить значение D.

с) Связать новый элемент со списком.

Ptr(p)=lst             (lst - уже не указывает на начало списка)

d) Перенести указатель lst на начало списка.

Окончательно:

Алгоритм

 

Наиболее рациональна реализация очередей в  виде  списковых структур данных.  Данная задача при ее реализации на ЭВМ дает большие навыки  при работе  со списковыми структурами  и при написании алгоритма программы следует воспользоваться стандартными  процедурами, такими  как  присоединение элемента в начало и конец списка, удаление  произвольного элемента из списка. Эти процедуры имеют следующий вид:

Алгоритм

Алгоритм  сортировки прямым включением таков:

                 for x:=2 to n do

                   x:=a[i]

                   включение х на соответствующее место среди a[1]...a[i]

                 end

В реальном процессе поиска подходящего места удобно, чередуя сравнения

сравнивается с очередным элементом a( j ), а затем либо х вставляется на свободное место, либо a( j ) сдвигается (передается) вправо и процесс "уходит" влево. Обратите внимание, что процесс просеивания может закончиться  при выполнении одного из двух следующих различных условий:

      1. Найден элемент a( j ) с ключом, меньшим, чем ключ у х.

      2. Достигнут левый конец готовой последовательности.

              Procedure StraightInsertion

               Var

                 i,j:index; x:item;

               begin

                 for i:=2 to n do

                   x:=a[i]; a[0]:=x; j:=1;

                   while x<a[j-1] do a[j-1]:=a[j-1]; j:=j-1; end;

                   a[j]:=x

                   end

               end StraightInsertion

Алгоритм

К прямым методам относится метод прямого выбора.

Рассматриваем весь ряд массива и выбираем элемент меньший или больший элемента а(i), определяем его место в массиве - k, и затем меняем местами элемент а(i) и элемент а(k).

for i = 1 to n - 1

  x = a(i)

  k = i

  for j = i + 1 to n

    if x > a(j) then

      k = j

      x = a(k)

    endif

  next j

  a(k) = a(i)

  a(i) = x

next i

return

for i := 1 to n - 1 do

  begin

    x := a[i];

    k := i;

    for j := i + 1 to n do

      if x > a[j] then

        begin

          k := j;

          x := a[k];

        end;

    a[k] := a[i];

    a[i] := x;

  end;

Эффективность алгоритма:

§       Количество сравнений

§       Количество перемещений, когда массив упорядочен

§       Количество перемещений когда массив обратно отсортирован

В худшем случае сортировка прямым выбором дает порядок n2, как и для числа сравнений, так и для числа перемещений.

Алгоритм

Для создания дерева необходимо создать в памяти элемент следующего типа :

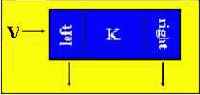
Тип на ПАСКАЛе :

           type

           pelem = ^elem;

           elem  = record

                           left : pointer;

                           right : pointer;

                           K : integer;

           end;

K - элемент массива, V - указатель на созданный элемент.

В процедуре создания дерева бинарного поиска будут использованы следующие указатели :

tree - указатель на корень дерева;

p - рабочий указатель;

q - указатель отстающий на шаг от p;

key - новый элемент массива;

Алгоритм

 

Рассмотрим алгоритм вставки узла в бинарное дерево.

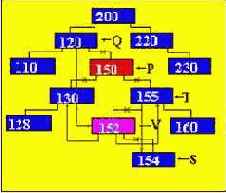
Вставим узел с номером 150, тогда он станет  правым сыном узла с номером   120, т.к. он  является большим по значению узла с номером 120, но меньше значения узла головы дерева.

 

   P - рабочий указатель

   Q - указатель  отстающий от Р на один шаг

   V - указатель на элемент, который будет вставлен в бинарное дерево .

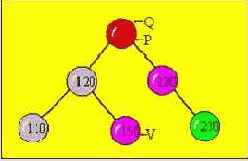
Иллюстрация процесса вставки  узла 150, в соответствии с вышеприведенным алгоритмом (красным цветом выделены новые связи в дереве).

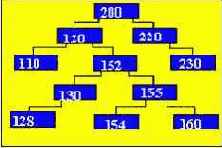
Конечный вариант дерева после вставки :

Программа

Псевдокод                               Паскаль

Q=nil                                  Q=nil

P=Tree                                 P=Tree

While (P<>nil) do                      While (P<>nil) do

Q=P                                  Begin

If key=k(P) then                       Q=P;

search=P                          If key=P^.k then

return                              Begin

EndIf                                    search:=P;

If key<k(P)  then                            exit;

P=left(P)                               End;

else                                   If key<P^.k then

P=right(P)                              P:=P^.left;

EndIf                                 else

EndWhile                                   P:=P^.right;

V=maketree(key,rec)                    End;

If key<k(Q) then                     V=maketree(key,rec)

else                                 If key<Q^.k then

Right(Q)=V                            Q^.left:=V

EndIf                                 else

search=V                               Q^.right:=V;

Return                                  search:=V

Алгоритм

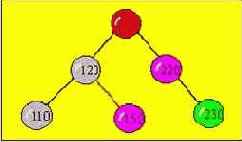
Рассмотрим алгоритм в котором  вместо удаляемого узла ставится  самый левый узел правого  поддерева. Удалим узел  с номером 150, тогда на его место станет элемент под номером 152, т.к. он  является самым  левым из правого поддерева.

Введем  следующие обозначения:

P - рабочий указатель

Q - указатель  отстающий от Р на один шаг

V - указатель на элемент, который будет замещать удаляемый узел

T - указатель, отстает от V на один шаг

S - указатель,  опережает V на один шаг

Пример программы удаления элементов бинарного дерева

(Псевдокод)

Q=nil

 P=Tree

 While (P<>nil)and(K(P)<>key)do {поиск узла с нужным ключем}

   If key<K(P) then P=Left(P)

     Else P=Right(P)

   EndIf

 EndWhile

 If P=nil then "Ключ не найден" {проверка если такого элемента нет}

                Return          {выход}

 EndIf

 If Left(P)=nil then V=Right(P) {если левая ссылка равна nil

   Else

     If Right(P)=nil then V=Left(P)

       Else

         GetNode(P)

         T=P

         V=Right(P) S = Left(V)

 While S <> nil  {поиск самого }

   T = V         {левого эл-нта}

   V = S     {правого поддерева}

   S = Left(V)

 EndWhile

 If T <> P then

   "V-не сын"

   Left(T) = Right(V)

   Right(V)= Right(P)

 EndIf

 Left(V) = Left(P)

 If Q = nil then

   "p - корень"

   Tree = V

   Return

 EndIf

       If P = Left(Q) then

         Left(Q) = V

       Else

         Right(Q)= V

       EndIf

     EndIf

   EndIf

 FreeNode(P)

Return

Иллюстрация процесса удаления узла 150, в соответствии с вышеприведенным алгоритмом (красным цветом выделены новые связи в дереве).

Конечный вариант дерева после удаления

 

Алгоритм

Если обнаруживается, что строка таблицы, соответствующая заданному ключу, не содержит желаемого элемента, то, значит, произошел конфликт, т. е. два элемента имеют такие ключи, которые отобра­жаются в один и тот же индекс. В этой ситуации нужна вторая попытка с индексом, вполне опреде­ленным образом получаемым из того же заданного ключа. Существует несколько методов формирования вторичного индекса. Очевидный прием — связывать вместе все строки с идентичным первичным индексом H(k). Превращая их в связанный список. Такой прием называется прямым связыванием (direct chaining). Элементы получающегося списка могут либо поме­щаться в основную таблицу, либо нет; в этом случае память, где они размещаются, обычно называется областью переполнения. Недостаток такого приема в том, что нужно следить за такими вторичными списками и в каждой строке отводить место для ссылки (или индекса) на соответствующий список конфликтующих элементов.

Другой прием разрешения конфликтов состоит в том, что мы совсем отказываемся от ссылок и вместо этого просматриваем другие строки той же таб­лицы — до тех пор, пока не обнаружим желаемый элемент или же пустую строку. В последнем случае мы считаем, что указанного ключа в таблице нет. Такой прием называется открытой адресацией. Естественно, что во второй попытке последователь­ность индексов должна быть всегда одной и той же для любого заданного ключа. В этом случае алгоритм просмотра строится по такой схеме:

h = H(k)

i = 0

repeat

   if T(h)  =  k 

then  элемент найден

else if T(h) = free

then элемента в таблице нет

else {конфликт}

i := i + 1

h := H(k) + G(i)

endif

   endif

until  либо найден, либо нет в таблице (либо она полна)

Предлагались самые разные функции G(i) для разрешения конфликтов. Приведенный в работе Морриса  (1968) обзор стимулировал активную деятельность в этом направлении. Самый простой прием — посмотреть следующую строку таблицы (будем считать ее круговой), и так до тех пор, пока либо будет найден элемент с указанным клю­чом, либо встретится пустая строка.

Алгоритм метода Quiksort

(ПСЕВДОКОД)

Sub Sort(L,R)

  i=l

  j=r

  x=A(( l+r ) div 2 )

       while A( i ) < x do

         i=i+1

     end while

     while A( j )>x do

         j=j-1

     end while

     if i<=j then

        Y=A( i )

        A( i )=A( j )

        A( j )=Y

      while i>j do

          if l<j then

            sort( l,j )

          end if

          if i<r then

            sort( i,r )

          end if

  return

sub Quiksort

   sort ( 1, n )

return

Число перестановок и сравнений: (n* log( n )).

Алгоритм пузырькового метода

(ПСЕВДОКОД)

for i=2 to n

  for j=n to i step -1

    if A( j-1 ) > A( j ) then

      x=A( j-1 )

      A( j-1 )=A( j )

      A( j )=x

    end if

next j

next i 

Алгоритм создания дерева бинарного поиска

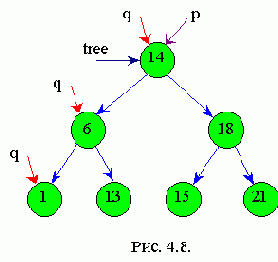
Пусть заданы элементы с ключами: 14, 18, 6, 21, 1, 13, 15. После выполнения нижеприведенного алгоритма получится дерево, изображенное на рис.4.6. Если обойти полученное дерево слева направо, то получим упорядочивание: 1, 6, 13, 14, 15, 18, 21.

Псевдокод read (key, rec) tree = maketree(key rec) p = tree q = tree while not eof do   read (key, rec)   v = maketree(key, rec)   while p <> nil do     q = p     if key < k(p) then       p = left(p)     else       p = right(p)     endif   endwhile     if key < k(q) then       left(p) = v     else       right(p) = v   endif     if q=tree then           ' только корень'     endif   return

Паскаль read (key, rec); tree := maketree(key rec); p := tree; q := tree; while not eof do   begin     read (key, rec);     v := maketree(key, rec);     while p <> nil do       begin         q := p;         if key < p^.k then           p := p^.left         else           p := p^.right;       end;       if key < q^.k then         p^.left := v       else         p^.right := v; end   if q=tree     then writeln(‘Только корень’); exit

Бинарные деревья

Бинарные деревья являются наиболее используемой разновидностью деревьев.

Согласно представлению деревьев в памяти ЭВМ каждый элемент будет записью, содержащей 4 поля. Значения этих полей будут соответственно ключ записи, ссылка на элемент влево-вниз, на элемент вправо-вниз и на текст записи.

При построении необходимо помнить, что левый сын имеет ключ меньший, чем у отца, а значение ключа правого сына больше значения ключа отца. Например, построим бинарное дерево из следующих элементов: 50, 46, 61, 48, 29, 55, 79. Оно имеет следующий вид:

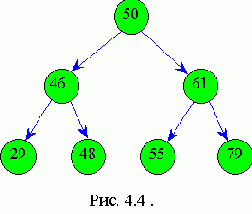
Получили упорядоченное бинарное дерево с одинаковым числом уровней в левом и правом поддеревьях. Это - идеально сбалансированное дерево, то есть дерево, в котором левое и правое поддеревья имеют уровни, отличающиеся не более чем на единицу.

Для создания бинарного дерева надо создавать в памяти элементы типа (рис. 4.5):

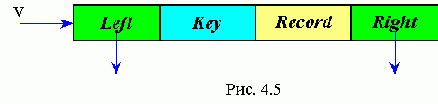
Операция V = MakeTree(Key, Rec) - создает элемент (узел дерева) с двумя указателями и двумя полями (ключевым и информационным) .

Вид процедуры MakeTree:

Псевдокод p = getnode r(p) = rec k(p) = key v = p left(p) = nil right(p) = nil

Паскаль New(p); p^.r := rec; p^.k := key; v := p; p^.left := nil; p^.right := nil;

Бинарный поиск (метод деления пополам)

Будем предполагать, что имеем упорядоченный по возрастанию массив чисел. Основная идея - выбрать случайно некоторый элемент AM и сравнить его с аргументом поиска Х. Если AM=Х, то поиск закончен; если AM <X, то мы заключаем, что все элементы с индексами, меньшими или равными М, можно исключить из дальнейшего поиска. Аналогично, если AM >X.

Выбор М совершенно произволен в том смысле, что корректность алгоритма от него не зависит. Однако на его эффективность выбор влияет. Ясно, что наша задача- исключить как можно больше элементов из дальнейшего поиска. Оптимальным решением будет выбор среднего элемента, т.е. середины массива.

Рассмотрим пример, представленный на рис. 5.7. Допустим нам необходимо найти элемент с ключом 52. Первым сравниваемым элементом будет 49. Так как 49<52, то ищем следующую середину среди элементов, расположенных выше 49. Это число 86. 86>52, поэтому теперь ищем 52 среди элементов, расположенных ниже 86, но выше 49. На следующем шаге обнаруживаем, что очередное значение середины равно 52. Мы нашли элемент в массиве с заданным ключом.

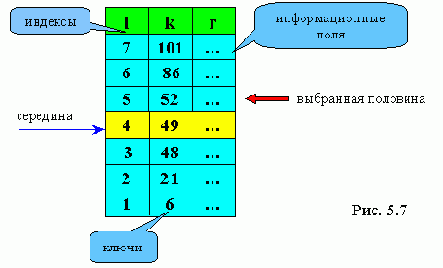
Программы на псевдокоде и Паскале:

Low = 1 hi = n while (low <= hi) do   mid = (low + hi) div 2   if key = k(mid) then     search = mid     return   endif   if key < k(mid) then     hi = mid - 1     else low = mid + 1   endif endwhile search = 0 return

low := 1; hi := n; while (low <= hi) do   begin     mid := (low + hi) div 2;     if key = k[mid] then       begin         search := mid;         exit;       end;     if key < k[mid]       then hi := mid - 1       else low := mid + 1;   end; search := 0; exit

При key = 101 запись будет найдена за три сравнения (в последовательном поиске понадобилось бы семь сравнений).

Если С - количество сравнений, а n - число элементов в таблице, то

С = log2n.

Например, n = 1024.

При последовательном поиске С = 512, а при бинарном

С = 10.

Можно совместить бинарный и индексно-последовательный поиск (при больших объемах данных), учитывая, что последний также используется при отсортированном массиве.

Быстрая сортировка (Quick Sort)

Относится к методам обменной сортировки. В основе лежит методика разделения ключей по отношению к выбранному.

Слева от 6 располагают все ключи с меньшими, а справа - с большими или равными 6 (рис. 6.4).

Sub Sort (L, R) i = L j = R x = a((L + R) div 2) repeat   while a(i) < x do     i = i + 1   endwhile   while a(j) > x do     j = j - 1   endwhile   if i <= j then     y = a(i)     a(i) = a(j)     a(j) = y     i = i + 1     j = j - 1   endif until i > j if L < j then   sort (L, j) endif if i < R then   sort (i, R) endif return sub QuickSort sort (1, n) return

procedure Sort (L, R: integer); begin   i := L;   j := r;   x := a[(L + r) div 2];   repeat     while a[i] < x do       i := i + 1;        while a[j] > x do       j := j - 1;     if i <= j then       begin         y := a[i];         a[i] := a[j];         a[j] := y;         i := i + 1;         j := j - 1       end;   until i > j;   if L < j then sort (L, j);   if i < r then sort (i, r); end;     procedure QuickSort; begin   sort (1, n); end;

Эффективность алгоритма:

О(n log n) - самый эффективный метод.

Целый тип - INTEGER

Этот тип включает некоторое подмножество целых, размер которого варьируется от машины к машине. Если для представления целых чисел в машине используется n разрядов, причем используется дополнительный код, то допустимые числа должны удовлетворять условию  -2 n-1<= x< 2 n-1.

Считается, что все операции над данными этого типа выполняются точно и соответствуют обычным правилам арифметики. Если результат выходит за пределы представимого множества, то вычисления будут прерваны. Такое событие называется переполнением.

Числа делятся на знаковые и беззнаковые. Для каждого из них имеется свой диапазон значений:

a)(0..2n-1) для беззнаковых чисел

b) (-2N-1.. 2N-1-1) для знаковых.

При обработке машиной чисел, используется формат со знаком. Если же машинное слово используется для записи и обработки команд и указателей, то в этом случае используется формат без знака.

Операции над целым типом:

a) Сложение.

b) Вычитание.

c) Умножение.

d) Целочисленное деление.

e) Нахождение остатка по модулю.

f) Нахождение экстремума числа (минимума и максимума)

g) Реляционные операции (операции сравнения) (<,>,<=, >=,=,<>)

Примеры:

A div B = C

A mod B = D

C * B + D = A

7 div 3 = 2

7 mod 3 = 1

Во всех операциях, кроме реляционных,  в результате получается целое число.

Дек

От английского DEQ - Double Ended Queue (Очередь с двумя концами)

Особенностью деков является то, что запись и считывание элементов может производиться с двух концов (рис. 2.18).

Дек можно рассматривать и в виде двух стеков, соединенных нижними границами. Возьмем пример, иллюстрирующий принцип построения дека. Рассмотрим состав на железнодорожной станции. Новые вагоны к составу можно добавлять либо к его концу, либо к началу. Аналогично, чтобы отсоединить от состава вагон, находящийся в середине, нужно сначала отсоединить все вагоны или вначале, или в конце состава, отсоединить нужный вагон, а затем присоединить их снова.

 

Операции над деками:

1. Insert - вставка элемента.

2. Remove - извлечение элемента из дека.

3. Empty - проверка на пустоту.

4. Full - проверка на переполнениe.

Контрольные  вопросы

        1.        Что такое  структуры  данных?

        2.        Назовите уровни  представления данных?

        3.        Какова классификация структур данных?

        4.        Какая статическая структура является самой простой?

        5.        Перечислите основные элементы таблицы.

        6.        Назовите их основные особенности.

        7.        Что такое вектор?

        8.        Что представляет из себя запись?

        9.        Какова структура записи?

     10.     К каким структурам данных относятся очереди и стеки ?

     11.     Каково правило выборки элемента из стека ?

     12.     Какая операция  читает верхний элемент стека без его удаления ?

     13.     Какую дисциплину обслуживания принято называть FIFO, а какую - LIFO ?

     14.     Признак заполнения кольцевой очереди ?

     15.     Признак пустой очереди ?

     16.     Что называется списком?

     17.     Перечислите виды списков.

     18.     Назовите элементы очереди.

     19.     Как организуется кольцевая очередь?

     20.     Какова особенность деков?

Деревья

 

Дерево - нелинейная связанная структура данных

(рис. 4.2).

Дерево характеризуется следующими признаками:

 - дерево имеет 1 элемент, на которого нет ссылок от других элементов. Этот элемент называется корнем дерева;

 - в дереве можно обратиться к любому элементу путем прохождения конечного числа ссылок (указателей);

 - каждый элемент дерева связан только с одним предыдущим элементом, Любой узел дерева может быть промежуточным либо терминальным (листом). На рис. 4.2 промежуточными являются элементы M1, M2, листьями - A, B, C, D, E. Характерной особенностью терминального узла является отсутствие ветвей.

Высота - это количество уровней дерева. У дерева на рис. 4.2 высота равна двум.

Количество ветвей, растущих из узла дерева, называется степенью исхода узла (на рис. 4.2 для M1 степень исхода 2, для М2 - 3). По степени исхода классифицируются деревья:

1) если максимальная степень исхода равна m, то это - m-арное дерево;

2) если степень исхода равна либо 0, либо m, то это - полное m-арное дерево;      

3) если максимальная степень исхода равна 2, то это - бинарное дерево;

4) если степень исхода равна либо 0, либо 2, то это - полное бинарное дерево.

Для описание связей между узлами дерева применяют также следующую терминологию: М1 - “отец” для элементов А и В. А и В - “сыновья” узла М1.

Дерево оптимального поиска

Если извлекаемые элементы сформировали некоторое постоянное множество, то может быть выгодным настроить дерево бинарного поиска для большей эффективности последующего поиска.

Рассмотрим деревья бинарного поиска, приведенные на рисунках a и b.Оба дерева содержат три элемента - к1, к2, к3, где к1<к2<к3. Поиск элемента к3

требует двух сравнений для рисунка 5.6 a), и только одного - для рисунка 5.6 б).

Число сравнений ключей, которые необходимо сделать для извлечения некоторой записи, равно уровню этой записи в дереве бинарного поиска плюс 1.

Предположим, что:

p1 - вероятность того, что аргумент поиска key = к1

р2 - вероятность того, что аргумент поиска key = к2

р3 - вероятность того, что аргумент поиска key = к3

q0 - вероятность того, что key < к1

q1 - вероятность того, что к2 > key > к1

q2 - вероятность того, что к3 > key > к2

q3 - вероятность того, что key > к3

C1 - число сравнений в первом дереве рисунка 5.6 a)

C2 - число сравнений во втором дереве рисунка 5.6 б)

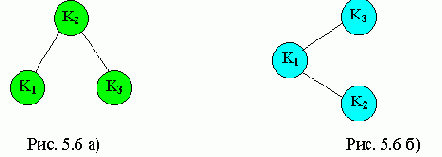
Тогда ?р1+?р2+?р3+?q0+?q1+?q2+?q3 = 1

Ожидаемое число сравнений в некотором поиске есть сумма произведений вероятности того, что данный аргумент имеет некоторое заданное значение, на число сравнений, необходимых для извлечения этого значения, где сумма берется по всем возможным значениям аргумента поиска. Поэтому

    C1 = 2?р1+1?р2+2?р3+2?q0+2?q1+2?q2+2?q3

         C2 = 2?р1+3?р2+1?р3+2?q0+3?q1+3?q2+1?q3

Это ожидаемое число сравнений может быть использовано как некоторая мера того, насколько "хорошо" конкретное дерево бинарного поиска подходит для некоторого данного множества ключей и некоторого заданного множества вероятностей. Так, для вероятностей, приведенных далее слева, дерево из a) является более эффективным, а для вероятностей, приведенных справа, дерево из б) является более эффективным:

                         P1 = 0.1                         P1 = 0.1

                         P2 = 0.3                         P2 = 0.1

                         P3 = 0.1                         P3 = 0.3

                         q0 = 0.1                         q0 = 0.1

                         q1 = 0.2                         q1 = 0.1

                         q2 = 0.1                         q2 = 0.1

                         q3 = 0.1                         q3 = 0.2

                         C1 = 1.7                        C1 = 1.9

                         C2 = 2.4                        C2 = 1.8

Дерево бинарного поиска, которое минимизирует ожидаемое число сравнений некоторого заданного множества ключей и вероятностей, называется оптимальным. Хотя алгоритм создания дерева может быть очень трудоемким, дерево, которое он создает, будет работать эффективно во всех последующих поисках. К сожалению, однако, заранее вероятности аргументов поиска редко известны.

Диапазонный или интервальный

В любом порядковом типе можно выделить подмножество значений, определяемое минимальным и максимальным значениями, в которое входят все значения исходного типа, находящиеся в этих границах, включая сами границы. Такое подмножество определяет диапазонный тип. Он задаётся указанием минимального и максимального значений, разделенных двумя точками.

TYPE T=[ MIN..MAX ]

TYPE <Час>=[1..60]

Минимальное значение при определении такого типа не должно быть больше максимального.

Контрольные  вопросы:

        1.        Каковы  основные характеристики  структур  данных?

        2.        Какие  типы  данных вы знаете ?

        3.        Какие из них относятся к стандартным, а  какие к пользовательским ?

        4.        Как представляются вещественные числа ?

        5.        Что представляют  собой  данные логического типа ?

        6.        Какие типы данных относятся к стандартным  пользовательским ?

        7.        Какому условию должны удовлетворять допустимые числа типа INTEGER ?

        8.        Какие операции можно производить над целыми числами ?

        9.        Перечислите булевские операции.

     10.     Какова структура типа CHAR ?

     11.     Какие операции возможны над данными этого типа ?

     12.     Что можно вычислить с помощью данных указательного типа ?

     13.     Что представляет собой перечисляемый тип данных?

     14.     Как задается диапазонный тип ?

Динамические структуры данных

До сих пор мы рассматривали только статические программные объекты. Однако использование при программировании только статических объектов может вызвать определенные трудности, особенно с точки зрения получения эффективной машинной программы. Дело в том, что иногда мы заранее не знаем не только размера значения того или иного программного объекта, но также и того, будет ли существовать этот объект или нет. Такого рода программные объекты, которые возникают уже в процессе выполнения программы или размер значений которых определяется при выполнении программы, называются динамическими объектами.

Динамические структуры данных имеют 2 особенности:

1) Заранее не определено количество элементов в структуре.

2) Элементы динамических структур не имеют жесткой линейной упорядоченности. Они могут быть разбросаны по памяти.

Чтобы связать элементы динамических структур между собой в состав элементов помимо информационных полей входят поля указателей (рис. 3.1) (связок с другими элементами структуры).

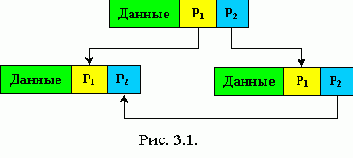
P1 и P2

это указатели, содержащие адреса элементов, с которыми они связаны. Указатели содержат номер слота.

Двусвязный список

Использование однонаправленных списков при решении ряда задач может вызвать определенные трудности. Дело в том, что по однонаправленному списку можно двигаться только в одном направлении, от заглавного звена к последнему звену списка. Между тем нередко возникает необходимость произвести какую-либо обработку элементов, предшествующих элементу с заданным свойством. Однако после нахождения элемента с этим свойством в односвязном списке у нас нет возможности получить достаточно удобный и быстрый доступ к предыдущим элементам- для достижения этой цели придется усложнить алгоритм, что неудобно и нерационально.

Для устранения этого неудобства добавим в каждое звено списка еще одно поле, значением которого будет ссылка на предыдущее звено списка. Динамическая структура, состоящая из элементов такого типа, называется двунаправленным или двусвязным списком.

Двусвязный список характеризуется тем, что у любого элемента есть два указателя. Один указывает на предыдущий элемент (обратный), другой указывает на следующий элемент (прямой) (рис. 3.4).

Фактически двусвязный список это два односвязных списка с одинаковыми элементами, записанных в противоположной последовательности.

Индексно-последовательный поиск

При таком поиске организуется две таблицы: таблица данных со своими ключами (упорядоченная по возрастанию) и таблица индексов, которая тоже состоит из ключей данных, но эти ключи взяты из основной таблицы через определенный интервал (рис. 5.3).

Сначала производится последовательный поиск в таблице индексов по заданному аргументу поиска. Как только мы проходим ключ, который оказался меньше заданного, то этим мы устанавливаем нижнюю границу поиска в основной таблице - low, а затем - верхнюю - hi , на которой ( kind > key ).

Например, key = 101.

Поиск идет не по всей таблице, а от low  до hi.

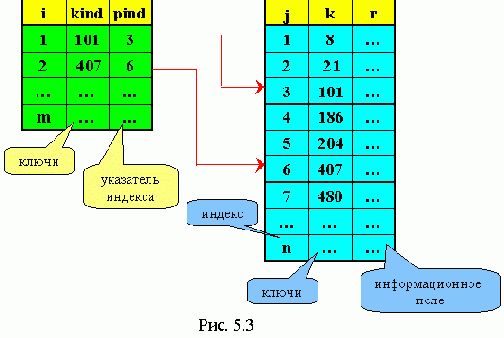
Примеры программ:

Псевдокод: i = 1 while (i <= m) and (kind(i) <= key) do   i=i+1 endwhile if i = 1 then low = 1   else low = pind(i-1) endif if i = m+1 then hi = n   else hi = pind(i)-1 endif for j=low to hi   if key = k(j) then     search=j     return   endif next j search=0 return

Паскаль: i:=1; while (i <= m) and (kind[i] <= key) do   i=i+1; if i = 1 then low:=1 else low:=pind[i-1]; if i = m+1 then hi:=n else hi:=pind[i]-1; for j:=low to hi do   if key = k[j] then     begin          search:=j;       exit;     end; search:=0; exit;

Эффективность индексно-последовательного поиска

Ecли  считать равновероятным появление всех случаев,то эффективность поиска можно рассчитать  следующим образом:

Введем  обозначения:  m - размер индекса;  m = n / p;

                                        p - размер шага

Q = (m+1)/2 + (p+1)/2 =  (n/p+1)/2 + (p+1)/2 = n/2p+p/2+1

Продифференцируем Q по p и приравняем производную нулю:

 

dQ/dp=(d/dp) (n/2p+p/2+1)= - n / 2 p2  +  1/2 = 0

    Отсюда

p2=n ;

   Подставив  ропт в выражение для Q, получим следующее количество сравнений:

    Q =

+1

Порядок  эффективности индексно-последовательного поиска O (

)

Эффективность последовательного поиска

Эффективность любого поиска может оцениваться по количеству сравнений C

аргумента поиска с ключами таблицы данных. Чем меньше количество сравнений, тем эффективнее алгоритм поиска.

Эффективность последовательного поиска в массиве:

C = 1 ? n, C = (n + 1)/2.

Эффективность последовательного поиска в списке - то же самое. Хотя по количеству сравнений поиск в связанном списке имеет ту же эффективность, что и поиск в массиве, организация данных в виде массива и списка имеет свои достоинства и недостатки. Целью поиска является выполнение следующих процедур:

1) Найденную запись считать.

2) При отсутствии записи произвести ее вставку в таблицу.

3) Найденную запись удалить.

Первая процедура (собственно поиск) занимает для них одно время. Вторая и третья процедуры для списочной структуры более эффективна (т. к. у массивов надо сдвигать элементы).

Если k - число передвижений элементов в массиве, то k = (n + 1)/2.

Элементы заголовков в списках

Для создания списка с заголовком в начало списка вводится дополнительный элемент, который может содержать информацию о списке (рис. 3.11).

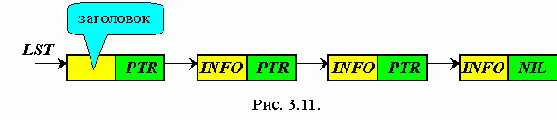
В заголовок списка часто помещают динамическую переменную, содержащую количество элементов  в списке (не считая самого заголовка).

Если список пуст, то остается только заголовок списка (рис. 3.12).

Также удобно занести в информационное поле заголовка значение указателя конца списка. Тогда, если список используется как очередь, то Fr = Lst, а    Re = Info(Lst).

Информационное поле заголовка можно использовать для хранения рабочего указателя при просмотре списка P = Info(Lst). То есть заголовок - это дескриптор структуры данных.

 

Классификация структур данных

Структуры данных классифицируются:

1. По связанности данных в структуре:

- если данные в структуре связаны очень слабо, то такие структуры называются несвязанными (вектор, массив, строки, стеки)

- если данные в структуре связаны, то такие структуры называются связанными (связанные списки)

2. По изменчивости структуры во времени или в процессе выполнения программы:

- статические структуры - структуры, неменяющиеся до конца выполнения программы (записи, массивы, строки, вектора)

- полустатические структуры (стеки, деки, очереди)

- динамические структуры - происходит полное изменение при выполнении программы

3. По упорядоченности структуры:

- линейные (вектора, массивы, стеки, деки, записи)

- нелинейные (многосвязные списки, древовидные структуры, графы)

Наиболее важной характеристикой является изменчивость структуры во времени.

Кольцевой двусвязный список

В программировании двусвязные списки часто обобщают следующим образом: в качестве значения поля Rptr последнего звена принимают ссылку на заглавное звено, а в качестве значения поля Lptr заглавного звена- ссылку на последнее звено. Список замыкается в своеобразное кольцо: двигаясь по ссылкам, можно от последнего звена переходить к заглавному и наоборот.

Операции над двусвязными списками:

  - cоздание элемента списка;

  - поиск элемента в списке;

  - вставка элемента в указанное место списка;

  - удаление из списка заданного элемента.

Кольцевой односвязный список

Кольцевой односвязный список получается из обычного односвязного списка путем присваивания указателю последнего элемента списка значение указателя начала списка (рис 3.3).

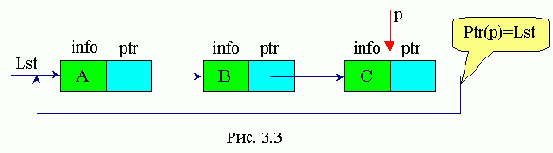
Простейшие операции, производимые над односвязными списками

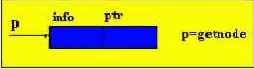
1) Вставка в начало односвязного списка.

Надо вставить в начало односвязного списка элемент с информационным полем D. Для этого необходимо сгенерировать пустой элемент (P=GetNode). Информационному полю этого элемента присвоить значение D (INFO(P)=D), значению указателя на этот элемент присвоить значение указателя на начало списка (Ptr(P) = Lst), значению указателя начала списка присвоить значение указателя P (Lst = P).

Реализация на Паскале:

type

  PNode = ^TNode;

  TNode = record

    Info: Integer;  {тип элементов списка - может быть любым}

    Next: PNode;

  end;

var

  Lst: PNode;  {указатель на начало списка}

  P: PNode;

Вставка в начало

New(P);   {создание нового элемента}

P^.Info:=D;

P^.Next:=Lst; {P указывает на начало списка, но Lst не указывает на   P - новое начало}

Lst:=P;  {Lst указывает на новое начало списка}

2) Удаление элемента из начала односвязного списка.

Надо удалить первый элемент списка, но запомнить информацию, содержащуюся в поле Info этого элемента. Для этого введем указатель P, который будет указывать на удаляемый элемент (P = Lst). В переменную X занесем значение информационного поля Info удаляемого элемента (X=Info(P)). Значению указателя на начало списка присвоим значение указателя следующего за удаляемым элемента (Lst = Ptr(P)). Удалим элемент (FreeNode(P)).

Реализация на Паскале:

Удаление из начала

P:=Lst;

X:=P^.Info;

Lst:=P^.Next;

Dispose(P);       {Удаляет элемент из динамической памяти}

Контрольный пример

Задание:

Дан список, содержащий имена студентов и соответствующие им баллы рейтинга. Необходимо отсортировать данный список по убыванию баллов рейтинга.

Сортировка методом прямого включения:

До сортировки		После сортировки
Аркадий		19		Артур		20
До сортировки		После сортировки
Мурат		17		Аркадий		19
Руслан		9		Александр		18
Артур		20		Владимир		18
Евгений		7		Мурат		17
Михаил		15		Казбек		16
Александр		18		Михаил		15
Виталий		14		Борис		15
Сидор		8		Денис		14
Владимир		18		Виталий		14
Алексей		6		Василий		13
Казбек		16		Петр		10
Марат		5		Руслан		9
Борис		15		Иван		8
Геннадий		2		Сидор		8
Денис		14		Евгений		7
Василий		13		Алексей		6
Сидор		3		Марат		5
Петр		10		Сидор		3
Иван		8		Геннадий		2

 

Краткая теория

Понятие очереди всем хорошо известно из повседневной жизни. Элементами очереди в общем случае являются заказы на то или иное обслуживание: выбить чек на нужную сумму в кассе магазина, получить нужную информацию в справочном бюро, выполнить очередную операцию по обработке детали на данном станке в автоматической линии и т.д.

В программировании имеется структура данных, которая называется очередь.  Эта структура данных используется, например, для моделирования реальных очередей с целью определения их характеристик (средняя длина очереди, время пребывания заказа в очереди и т.п.) при данном законе поступления заказов и дисциплине их обслуживания.

По своему существу очередь является полустатической структурой - с течением времени и длина очереди, и набор образующих ее элементов могут изменяться.

Различают два основных вида очередей, отличающихся по дисциплине обслуживания находящихся в них элементов :

1.   При первой из дисциплин заказ, поступивший в очередь первым, выбирается первым для обслуживания (и удаляется из очереди). Эту дисциплину обслуживания принято называть FIFO (First input-First output, т.е. первый пришел - первый ушел). Очередь открыта с обеих сторон.

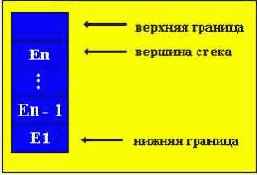
2.   Вторую дисциплину принято называть LIFO (Last input - First output, т.е. последний  пришел - первый ушел), при которой на обслуживание первым выбирается тот элемент очереди, который поступил в нее последним. Очередь такого вида в программировании принято называть СТЕКОМ (магазином) - это одна из наиболее употребительных структур данных, которая оказывается весьма удобной при решении различных задач.

В силу указанной дисциплины обслуживания, в стеке доступна единственная его позиция, которая называется ВЕРШИНОЙ стека - эта позиция, в которой находится последний по времени поступления в стек элемент. Когда мы заносим новый элемент в стек, то он помещается поверх вершины и теперь уже сам находится в вершине стека. Выбрать элемент можно только из вершины стека; при этом выбранный элемент исключается из стека, а в его вершине оказывается элемент, который был занесен в стек перед выбранным из него элементом (структура с ограниченным доступом к данным).

 

До сих пор мы рассматривали только статические программные объекты. Этим термином обозначаются объекты, которые порождаются непосредственно перед выполнением программы, существуют в течение всего времени ее выполнения и размер значений которых не изменяется по ходу выполнения программы.

Поскольку статические объекты порождаются до выполнения программы и размер их значений можно выделить еще на этапе трансляции исходного текста программы на языке машины.

Однако использование при программировании только статических объектов может вызвать определенные трудности, особенно с точки зрения получения эффективной машинной программы, а такая эффективность бывает чрезвычайно важной при решении ряда задач. Дело в том, что иногда мы заранее не знаем не только размера значения того или иного программного объекта, но даже и того, будет существовать этот объект или нет. Такого рода программные объекты , которые возникают уже в процессе  выполнения программы, называют динамическими объектами.

В языке ПАСКАЛЬ для работы с динамическими объектами предусматривается специальный тип данных - так называемый ссылочный тип. Значением этого типа является ссылка на какой - либо программный объект, по которой осуществляется непосредственный доступ к этому объекту. На машинном языке такая ссылка как раз и представляется указанием места в памяти соответствующего объекта.

В этом случае для описания действий над динамическими объектами каждому такому объекту в программе сопоставляется статическая переменная ссылочного типа - в терминах этих ссылочных переменных и описываются действия над соответствующими динамическими объектами.

Итак, динамические структуры данных имеют две особенности :

 1. Заранее не определимо количество элементов в структуре;

 2. Элементы динамической структуры не имеют жесткой линейной упорядоченности. Они могут быть разбросаны по памяти.

Чтобы связать элементы динамической структуры между собой, в состав элемента помимо информационного поля входят поля указателей (связок с другими элементами структуры) .

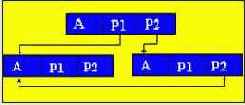
p1, p2 - указатели, содержащие адреса элементов, с которыми данный элемент связан.

Наиболее распространенными динамическими структурами являются связанные списки. С точки зрения логического представления различают линейные и нелинейные списки. В линейных списках связи строго упорядочены.  Указатель предыдущего элемента дает адрес последующего элемента или наоборот.

К линейным спискам относятся односвязные и двусвязные списки.

К нелинейным - многосвязные списки.

Элемент списка в общем случае представляет собой комбинацию поля записи (информационного поля) и одного или нескольких указателей.

О том, что из себя представляют списки говорилось в предыдущей работе. Мы рассматривали однонаправленные списки, теперь мы рассмотрим кольцевые списки.

Как видно на рисунке, список замыкается в своеобразное "кольцо": двигаясь по ссылкам, можно от последнего элемента списка переходить к заглавному элементу. В связи с этим списки подобного рода называют кольцевыми списками.

Чтобы закольцевать список необходимо присвоить указателю последнего элемента указатель начала списка (Ptr(p)=lst).

Ptr(p) - указатель последнего элемента;

Lst - указатель начала списка.

Формулировка задачи.

Пусть обслуживающая система состоит из конечного числа обслуживающих аппаратов. Система  относится к  числу систем с ожиданием. Каждый аппарат может обслуживать  одновременно  только   одно  требование. Если в момент поступления очередного требования  имеются  свободные  аппараты,  то один из них немедленно  приступает  к  обслуживанию, если свободных  аппаратов нет,  то   требование   ждет   обслуживания.  Естественно,   если   требований больше, чем обслуживающих аппаратов,  то образуется  очередь. Время  обслуживания одного требования есть  случайная  величина,  подчиненная  показательному закону распределения:

F(t)=1-e-nt

Поток поступающих требований ограничен, то есть одновременно в системе обслуживания не может находиться больше  m требований,  где m -  конечное число. Это дает право считать, что требования на  обслуживание поступают от m обслуживаемых объектов, которые время от времени нуждаются в  обслуживании.    Пусть вероятность того, что поступит заявка на обслуживания  на данном такте  равна  Р(А)  и  вероятность   того, что  требование  из  очереди поступит  на обслуживание равно Р(В) ( на каждом такте может поступить не  более   одной заявки  на обслуживание). Число обслуживающих аппаратов равно N.  Допустим,  требование дождалось своей очереди и оно начало обслуживаться. Обслуживание может длиться в течении не более 3-х тактов.  Заявки могут быть двух приоритетов:

Заявка первого приоритета:

     Это обычная заявка, она не обладает ни какими  привилегиями. Она  может покинуть систему через определенное число тактов Т. При приходе  в обслуживающую систему заявка первого  приоритета  становится в   конец очереди.

Заявка второго приоритета:

     Эта заявка отличается только тем, что она при поступлении в  обслуживающую систему   становится в начало очереди, то есть как только освобождается аппарат, то она поступает на обслуживание  с  вероятностью Р(В).

Заявка второго  приоритета , как и заявка первого  приоритета, покидает систему через Т тактов. Естественно, что появление заявок второго приоритета достаточно мало ( хотя эта вероятность задается пользователем и может быть любой ).  Теперь об обслуживании:    Количество тактов, в течение которых будет обслуживаться  та или иная заявка выбирается случайно (эта величина в  данной  задаче не должна быть больше 3).   Если заявка  обслужилась  положенное ей число тактов, то  она покидает систему. Если заявка находится в очереди больше Т тактов, то она с некоторой  вероятностью покидает систему. 

 

Общие сведения о структуре данных – дерево.

Дерево - это нелинейная связанная структура данных, характеризуемая следующими признаками :

дерево имеет один элемент, на который нет ссылок от других элементов. Этот элемент, или "узел", называется корнем дерева;

в дереве можно обратиться к любому элементу путем прохождения конечного числа ссылок (указателей) ;

каждый элемент дерева связан только с одним предыдущим элементом.

Каждый узел дерева может быть промежуточным (элементы 2,3,5,7) либо терминальным ("листом" дерева) (элементы 4,9,10,11,8,6). Характерной особенностью терминальных узлов является отсутствие ветвей.

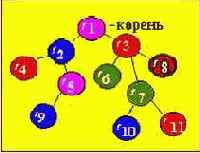
Элемент Y, находящийся непосредственно ниже элемента X, называется непосредственным потомком X, если X находится на уровне i , то говорят, что Y лежит на уровне i+1.

Считается, что корень лежит на уровне 0.

Число непосредственных потомков элемента называется его степенью исхода, в зависимости от степени исхода узлов деревья классифицируют :

A) Если степень исхода узлов - М, то дерево называется М-арным ;

B) Если степень исхода узлов - М или 0, то - полное М-арное дерево;

C) Если степень исхода узлов дерева равна 2, то дерево называется бинарным ;

D) Если степень исхода равна 2 или 0, то - полное бинарное дерево.

Особенно важную роль играют бинарные деревья, далее мы будем рассматривать их более подробно.

Представление деревьев в памяти ЭВМ

Деревья наиболее удобно представлять в памяти ЭВМ в виде связанных нелинейных списков. Элемент должен содержать INFO-поле, где содержится характеристика узла. Следующее поле определяет степень исхода узла и количество полей указателей равное степени исхода. Каждый указатель элемента ориентирует данный элемент-узел с его сыновьями. Узлы, в которые входят стрелки от исходного элемента, называются его сыновьями.

INFO-поле содержит два поля : поле записи (rec) и поле ключа (key). Ключ задается числом, по ключу определяют место элемента в дереве.

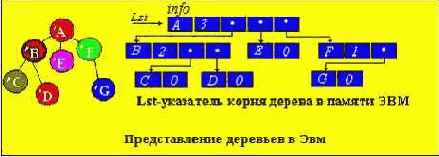
Сведение М-арного дерева к бинарному

При обработке данных в ЭВМ важно знать и информационное поле элемента, и его размещение в памяти машины. Для этих целей используется сортировка. Итак, сортировка- -это расположение данных в памяти в регулярном виде по их ключам. Регулярность рассматривают как возрастание значения ключа от начала к концу в массиве.

      Различают следующие типы сортировок:

§       внутренняя сортировка - это сортировка, происходящая в оперативной памяти машины

§       внешняя сортировка - сортировка во внешней памяти.

Если сортируемые записи занимают большой объем памяти, то их перемещение требует больших затрат. Для того, чтобы их уменьшить, сортировку производят в таблице адресов ключей, делают перестановку указателей, т.е. сам массив не перемещается. Это метод сортировки таблицы адресов.

При сортировке могут встретиться одинаковые ключи. В этом случае при сортировке желательно расположить после сортировки одинаковые ключи в том же расположении, что и в исходном файле. Это устойчивая сортировка.

Эффективность сортировки можно рассмотреть с нескольких критериев:

§       время, затрачиваемое на сортировку

§       объем оперативной памяти, требуемой для сортировки

§       время, затраченное программистом на написание программы

Рассмотрим второй критерий подробнее: мы можем подсчитать количество сравнений при выполнении сортировки или количество перемещений.

         Предположим, что число сравнений определяется формулой:

C = 0,01n2 + 10n

Если n<1000, то второе слагаемое больше.

Если n>1000, то первое слагаемое больше.

То есть, при малых n порядок сравнения равен , а при больших n он равен n.

Различают следующие методы сортировки:

§       строгие (прямые) методы

§       улучшенные методы

Рассмотрим преимущества прямых методов:

1.

 

В общем сортировку следует понимать как процесс перегруппировки заданного множества объектов в некотором определенном порядке. Цель сортировки облегчить последующий  поиск элементов в таком отсортированном множестве. Это почти универсальная, фундаментальная деятельность. Мы встречаемся с отсортированными объектами в телефонных книгах, в списках подоходных налогов, в оглавлениях книг, в библиотеках, в словарях, на складах почти везде, где нужно искать хранимые объекты. Даже малышей учат держать свои вещи "в порядке", и они уже сталкиваются с некоторыми видами сортировок задолго до того, как познакомятся с азами арифметики.    

Таким образом, разговор о сортировке вполне уместен и важен, если речь идет об обработке данных. Что может легче сортироваться, чем данные? Тем не менее наш первоначальный интерес к сортировке основывается на том, что при построении алгоритмов мы сталкиваемся со многими весьма фундаментальными приемами. Почти не существует методов, с которыми не приходится встречаться при обсуждении этой задачи. В частности, сортировка это идеальный объект для демонстрации огромного разнообразия алгоритмов, все они изобретены для одной и той же задачи, многие в некотором смысле оптимальны, большинство имеет свои достоинства. Поэтому это еще и идеальный объект, демонстрирующий необходимость анализа производительности алгоритмов. К тому же на примерах сортировок можно показать, как путем усложнения алгоритма, хотя под рукой и есть уже очевидные методы, можно добиться значительного выигрыша в эффективности.

Выбор алгоритма зависит от структуры обрабатываемых данных это почти закон, но в случае сортировки такая зависимость столь глубока, что соответствующие методы были даже разбиты на два класса сортировку массивов и сортировку файлов последовательностей . Иногда их называют внутренней и внешней сортировкой, поскольку массивы хранятся в быстрой оперативной, внутренней  памяти машины со случайным доступом, а файлы обычно размещаются в более медленной, но и более емкой внешней памяти, на устройствах, основанных на механических перемещениях дисках или лентах .

 

Пузырьковая сортировка

Идея : (N-1) раз массив проходится снизу вверх (сверху вниз), при этом элементы попарно сравниваются, если нижний элемент меньше верхнего, то элементы переставляются.

Пример : массив - 4, 3, 7, 2, 1, 6.

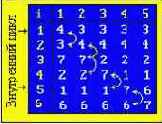
Можно улучшить "пузырьковый" метод, если проходить массив элементов и вверх и вниз одновременно.

Количество сравнений :

Количество перемещений :

Пример вычисления "пузырьковым" методом

 

 

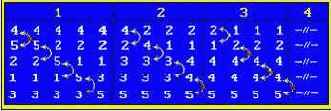
На примере представлен массив из пяти элементов, это означает, что массив проходится снизу вверх (сверху вниз) 5-1=4 раза. Так же на примере видно, что алгоритм "в пустую" обрабатывает массив начиная уже с третьего шага внутреннего цикла, а 4-й шаг можно уже не выполнять.

Преимущества данного метода :

1) Самый простой алгоритм

2) Простой в реализации

3) Не нужно дополнительных переменных

  Недостатки:

1) Долго обрабатывает большие массивы

2) В любом случае количество проходов не уменьшается

Quiksort - метод быстрой сортировки

Идея : В основе данного метода положен метод разделение ключей по отношению к выбранному.

Пример :

 

 

После первого прохода выбранный элемент становится на свое место.

Улучшение "пузырькового" метода.

1) Если проходить массив не только сверху вниз, но и снизу вверх одновременно, то не только "легкие" элементы  будут "всплывать", но и "тяжелые" "тонуть".

2)   Для отмены прохода массива "впустую" нужно в во внешний цикл вставить проверку на отсортированность массива.

 

При обработке данных в ЭВМ важно знать и информационное поле элемента, и его размещение в памяти машины. Для этих целей используется сортировка. Итак, сортировка - это расположение данных в памяти в регулярном виде по их ключам. Регулярность рассматривают как возрастание значения ключа от начала к концу в массиве.

Различают следующие типы сортировок:

внутренняя сортировка - это сортировка, происходящая в оперативной памяти машины

внешняя сортировка - сортировка во внешней памяти.

Схематичное представление двоичного дерева :                       имеется набор вершин, соединенных стрелками. Из каждой вершины выходит не более двух стрелок (ветвей ), направленных влево - вниз или вправо - вниз. Должна существовать единственная вершина, в которую не входит ни одна стрелка - эта вершина называется корнем дерева. В каждую из оставшихся вершин входит одна стрелка.

Существует множество способов упорядочивания дерева. Рассмотрим один из них :

       " Левый " сын имеет ключ меньше, чем ключ " Отца "

       " Правый " сын имеет ключ больше, чем ключ " Отца "

Получили бинарное упорядоченное дерево с минимальным числом уровней.

Строго сбалансированное дерево : дерево, в котором левое и правое поддерево имеют  уровни , отличающиеся  не более, чем на единицу.

Рассмотрим принцип построения дерева при занесении элементов в массив :

Пусть в первоначально пустой массив заносятся последовательно поступающие элементы :  70, 60, 85, 87, 90, 45, 30, 88, 35, 20, 86 ; Т.к. это еще пустое дерево, то ссылки left и right равны  nil( left - указатель на левого сына (элемент), right - указатель на правого сына (элемент)).

Четвертый из поступающих элементов 87. Т.к. этот ключ больше ключа 70 ( корень ), то новая вершина должна размещаться на правой ветви дерева. Чтобы определить ее место, спускаемся по правой стрелке к очередной вершине ( с ключом 85 ), и если поступивший ключ больше 85, то новую вершину делаем правым сыном вершины с ключом 85 .

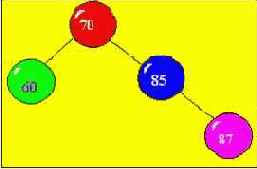
В рассмотренном примере ПРИНЦИП ПОСТРОЕНИЯ ДЕРЕВА имеет следующий вид : если поступает очередной элемент массива, то начиная с корня дерева (в зависимости от сравнения текущего элемента с очередной вершиной) идем влево или вправо от нее до тех пор, пока не найдем подходящую вершину, к которой можно подключить новую вершину с текущим ключом. В зависимости от результата сравнения ключей, новую вершину делаем левой или правой для найденной вершины.

 

ПОИСК

Одно из наиболее часто встречающихся в программировании действий - поиск. Он же представляет собой идеальную задачу, на которой можно испытывать различные структуры данных по мере их появления. Существует несколько основных "вариаций этой темы", и для них создано много различных алгоритмов. При дальнейшем рассмотрении мы исходим из такого принципиального допущения: группа данных, в которой необходимо отыскать заданный элемент, фиксирована. Будем считать, что множество из N элементов задано, скажем, в виде такого массива

a: ARRAY[0..N-1] OF item

Обычно тип item описывает запись с некоторым полем, выполняющим роль ключа. Задача заключается в поиске элемента, ключ которого равен заданному "аргументу поиска" x. Полученный в результате индекс i, удовлетворяющий условию a[i].key=x, обеспечивает доступ к другим полям обнаруженного элемента. Так как нас интересует в первую очередь сам процесс поиска, а не обнаруженные данные, то мы будем считать, что тип item включает только ключ, т.е. он есть ключ (key).

ПОИСК (SEARCH) является одной из основ обработки данных в ЭВМ. Его назначение состоит в том, чтобы по заданному аргументу найти среди массива данных те данные, которые соответствуют этому аргументу или определить, что этих данных нет. Если этих данных нет, добавить их в массив данных.

Набор любых данных будем называть ТАБЛИЦЕЙ или ФАЙЛОМ. Данное или элемент структуры отличается каким-то признаком от других данных. Этот признак называется КЛЮЧОМ. Ключ может быть УНИКАЛЬНЫМ, т.е. в таблице только одно данное с таким ключом, иначе уникальные ключи называются ПЕРВИЧНЫМИ КЛЮЧАМИ.

ВТОРИЧНЫЙ КЛЮЧ в одной таблице может повторяться, но по нему тоже можно организовать поиск. Ключи данных собраны в одном месте (таблице).

Ключи, которые выделены из таблицы данных и организованы в свой файл, называются ВНЕШНИМИ КЛЮЧАМИ. Если ключ в записи, то он называется ВНУТРЕННИМ КЛЮЧОМ.

ПОИСКОМ ПО ЗАДАННОМУ АРГУМЕНТУ называется алгоритм, определяющий соответствие ключа данного с заданным аргументом. Результатом работы алгоритма поиска может быть нахождение этого данного или отсутствие данного в таблице. В случае отсутствия данного возможны две операции:

       1. Индикация того, что данного нет.

       2. Вставка данного в таблицу.

Пусть К - массив ключей, тогда для всех К(i) существует R(i) - данное. KEY - аргумент поиска. Ему соответствует информационная запись REC. В зависимости от того, какова структура данных в таблице, различают несколько видов поиска.

ПЕРЕУПОРЯДОЧЕНИЕ   ТАБЛИЦЫ  ПОИСКА

Всегда можно говорить о некотором значении вероятности  нахождения того или иного элемента.

P(i) - вероятность нахождения элемента.

В этом случае таблица поиска представляется как система с дискретными состояниями, а искомый элемент характеризуется i-ым состоянием системы, вероятность которого P(i).

P(1) + P(2) + ... + P(n) = 1

Количество сравнений Z при поиске в таблице, т.е. количество сравнений, необходимых для поиска по заданному аргументу, представляет собой значение дискретной случайной величины, определяемой номерами состояний и вероятностями состояний системы.

Z=1*P(1) + 2*P(2) + 3*P(3) + ... + n*P(n)

ТАБЛИЦА ДАННЫХ ДОЛЖНА БЫТЬ УПОРЯДОЧЕНА ТАКИМ ОБРАЗОМ , чтобы в начале таблицы были элементы с большими вероятностями поиска или элементы , к которым чаще всего обращаются в таблице.

P(1) >= P(2) >= P(3) >= ... >= P(n)

ИМЕЕТСЯ ДВА ОСНОВНЫХ МЕТОДА ПЕРЕУПОРЯДОЧЕНИЯ ТАБЛИЦ  ПОИСКА:

1.   Переупорядочение путем перестановки  найденного элемента в начало списка.

2.   Метод транспозиции.

ПОИСК ПО БИНАРНОМУ ДЕРЕВУ

Для вставки элемента в дерево сначала нужно осуществить поиск в дереве по заданному ключу. Если такой ключ имеется, то программа завершается, если нет то происходит вставка. Длительность операции поиска (число узлов, которые надо перебрать для этой цели) зависит от структуры дерева. Действительно, деревом может быть вырождено в однонаправленный список (иметь единственную ветвь) - такое дерево может возникнуть, если элементы поступали в дерево в порядке возрастания (убывания) их, ключей. В этом случае время поиска будет такое же, как и однонаправленном списке, т.е. в среднем придется перебрать N/2  элементов. Наибольший эффект использования дерева достигается в том случае, когда дерево "сбалансировано". В этом случае для поиска придется перебрать не более log2N.

ВКЛЮЧЕНИЕ ЭЛЕМЕНТА В ДЕРЕВО

Для включения новой записи в дерево, прежде всего нужно найти тот узел, к которому можно "подвесить"(присоединить) новый элемент. Алгоритм поиска нужного узла тот же самый, что и при поиске узла с заданным ключом. Этот узел будет найден в тот момент, когда в качестве очередной ссылки, определяющий ветвь дерева, в которое надо продолжить поиск, окажется ссылка NIL.

  Однако, непосредственно использовать процедуру поиска     нельзя, потому что по окончанию вычисления ее значение не  фиксирует тот узел, из которого была выбрана ссылка NIL. Модифицируем описание процедуры поиска так, чтобы в качестве ее побочного эффекта фиксировалась ссылка на узел, в котором был найден заданный ключ (в случае успешного поиска), или ссылка на узел, после обработки которого поиск прекращен (в случае неуспешного поиска).

Удаление узла дерева не должно нарушать упорядоченность дерева. При удалении возможны следующие варианты расположения узлов:

1)  найденный узел является листом - он просто удаляется (рис.1);

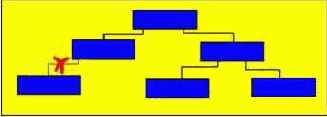
2)  найденный узел имеет только сына - в этом случае сын перемещается на место удаленного отца (рис.2);

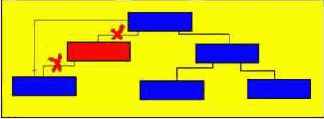
3)  у удаляемого отца два сына -  в  этом  случае  основная  трудность  состоит  в  удалении отца, поскольку в  удаляемую  вершину  входит одна  стрелка,  а выходит две.

В  этом случае  нужно найти  подходящее  звено  поддерева, которое можно было бы  вставить  на место удаляемого, причем  это  подходящее  звено должно просто  перемещаться. Такое  звено всегда  существует:

       - это самый  правый элемент   левого   поддерева  (для  достижения  этого  звена необходимо  перейти в следующую вершину по  левой ветви, а  затем  переходить в  очередные вершины  только  по правой ветви  до тех  пор, пока очередная ссылка не будет равна nil);

       - это самый  левый  элемент  правого  поддерева   (для  достижения  этого  звена необходимо перейти в следующую  вершину по правой ветви, а  затем  переходить  в очередные  вершины  только по левой ветви  до  тех  пор, пока  очередная такая ссылка не будет равна nil).

       Очевидно, что   такие  подходящие  звенья  могут  иметь  не  более  одной ветви.

 

При обработке данных важно знать и информационное поле данных, и размещение их в машине.

Различают внутреннюю и внешнюю сортировки:

-   внутренняя сортировка - сортировка в оперативной памяти;

-   внешняя сортировка - сортировка во внешней памяти.

Сортировка - это расположение данных в памяти в регулярном виде по их ключам. Регулярность рассматривают как возрастание (убывание) значения ключа от начала к концу в массиве.

Если сортируемые записи занимают большой объем памяти, то их перемещение требует больших затрат. Для того, чтобы их уменьшить, сортировку производят в таблице адресов ключей, делают перестановку указателей, т.е. сам массив не перемещается. Это метод сортировки таблицы адресов.

При сортировке могут встретиться одинаковые ключи. В этом случае при сортировке желательно расположить после сортировки одинаковые ключи в том же порядке, что и в исходном файле. Это устойчивая сортировка.

Эффективность сортировки можно рассматривать с нескольких критериев:

-   время, затрачиваемое на сортировку;

-   объем оперативной памяти, требуемой для сортировки;

-   время, затраченное программистом на написание программы.

Выделяем первый критерий. Можно подсчитать количество сравнений при выполнении сортировки или количество перемещений.

Пусть Н = 0,01n2 + 10n - число сравнений. Если n < 1000, то второе слагаемое больше, если n > 1000, то больше первое слагаемое.

Т. е. при малых n порядок сравнения будет равен n2, при больших n порядок сравнения - n.

Порядок сравнения при сортировке лежит в пределах

от 0 (n log n)  до 0 (n2); 0 (n) - идеальный случай.

Различают следующие методы сортировки:

-   строгие (прямые) методы;

-   улучшенные методы.

Строгие методы:

 1) метод прямого включения;

 2) метод прямого выбора;

 3) метод прямого обмена.

Количество перемещений в этих трех методах примерно одинаково.

   3.2.1 Сортировка методом прямого включения

Лабораторная работа № "БИНАРНЫЕ ДЕРЕВЬЯ(основные процедуры)"

Цель работы:

исследовать и изучить процедуры, используемые при работе с бинарными (двоичными) деревьями.

Задача работы:

овладеть навыками написания программ по исследованию бинарных деревьев .

Порядок работы :

q       изучить описание лабораторной работы;

q       по заданию, данному преподавателем, разработать алгоритм программы решения задачи;

q       написать программу на языке ПАСКАЛЬ;

q       отладить программу;

q       решить задачу;

q       оформить отчет.

Лабораторная работа № . "ИССЛЕДОВАНИЕ МЕТОДОВ ЛИНЕЙНОГО И БИНАРНОГО ПОИСКА"

Цель работы: изучить методы линейного и бинарного поиска.

Задача работы:

овладеть навыками написания программ для методов линейного и бинарного поиска на языке программирования ПАСКАЛЬ .

Порядок работы :

q       изучить описание лабораторной работы;

q       по заданию, данному преподавателем, разработать алгоритм программы решения задачи;

q       написать программу на языке ПАСКАЛЬ;

q       отладить программу;

q       решить задачу;

q       оформить отчет.

Цель работы:

исследовать и изучить методы поиска с перемещением в начало и транспозицией.

Задача работы:

овладеть навыками написания программ по исследованию методов поиска с перемещением в начало и транспозицией  на языке программирования ПАСКАЛЬ .

Порядок работы :

q       изучить описание лабораторной работы;

q       по заданию, данному преподавателем, разработать алгоритм программы решения задачи;

q       написать программу на языке ПАСКАЛЬ;

q       отладить программу;

q       решить задачу;

q       оформить отчет.

Лабораторная работа № "КОЛЬЦЕВЫЕ СПИСКИ"

Цель работы: исследовать и изучить кольцевые списки на примере основных процедур.

Задача работы: овладеть навыками написания программ по исследованию основных процедур списковых структур на языке программирования ПАСКАЛЬ .

Порядок работы :

q       изучить описание лабораторной работы;

q       по заданию, данному преподавателем, разработать алгоритм программы решения задачи;

q       написать программу на языке ПАСКАЛЬ;

q       отладить программу;

q       решить задачу;

q       оформить отчет.

Лабораторная работа № "МОДЕЛЬ МАССОВОГО ОБСЛУЖИВАНИЯ"

Цель работы: исследовать и изучить применение списковых структур данных при моделировании систем массового обслуживания.

Задача работы: овладеть навыками написания программ для теории массового обслуживания на языке программирования ПАСКАЛЬ .

Порядок работы :

q       изучить описание лабораторной работы;

q       по заданию, данному преподавателем, разработать алгоритм программы решения задачи;

q       написать программу на языке ПАСКАЛЬ;

q       отладить программу;

q       решить задачу;

q       оформить отчет.

Лабораторная работа № . "ПОИСК ПО ДЕРЕВУ С ВКЛЮЧЕНИЕМ"

Цель работы:

освоить алгоритм  и  метод вставки элементов бинарного дерева.

Задача работы:

овладеть навыками написания программ по исследованию методов вставки элементов бинарного дерева на языке программирования ПАСКАЛЬ .

Порядок работы :

q       изучить описание лабораторной работы;

q       по заданию, данному преподавателем, разработать алгоритм программы решения задачи;

q       написать программу на языке ПАСКАЛЬ;

q       отладить программу;

q       решить задачу;

q       оформить отчет.

Лабораторная работа № "ПОЛУСТАТИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ"

Цель работы: исследовать и изучить стеки.

Задача работы: овладеть навыками написания программ по исследованию стеков на языке программирования ПАСКАЛЬ .

Порядок работы :

q       изучить описание лабораторной работы;

q       по заданию, данному преподавателем, разработать алгоритм программы решения задачи;

q       написать программу на языке ПАСКАЛЬ;

q       отладить программу;

q       решить задачу;

q       оформить отчет.

Лабораторная работа № . "СОРТИРОВКА МЕТОДОМ ПРЯМОГО ВКЛЮЧЕНИЯ"

Цель работы:

исследовать и изучить методы сортировки включением.

Задача работы:

овладеть навыками написания программ для сортировки методом прямого включения на языке программирования ПАСКАЛЬ .

Порядок работы :

q       изучить описание лабораторной работы;

q       по заданию, данному преподавателем, разработать алгоритм программы решения задачи;

q       написать программу на языке ПАСКАЛЬ;

q       отладить программу;

q       решить задачу;

q       оформить отчет.

Лабораторная работа № "СОРТИРОВКА С ПОМОЩЬЮ ПРЯМОГО ОБМЕНА"

Цель работы:

исследовать и изучить методы сортировки с помощью прямого обмена.

Задача работы:

овладеть навыками написания программ для сортировки с помощью прямого обмена на языке программирования ПАСКАЛЬ .

Порядок работы :

q       изучить описание лабораторной работы;

q       по заданию, данному преподавателем, разработать алгоритм программы решения задачи;

q       написать программу на языке ПАСКАЛЬ;

q       отладить программу;

q       решить задачу;

q       оформить отчет.

Лабораторная работа № "СОРТИРОВКА С ПОМОЩЬЮ ДЕРЕВА"

Цель работы:

исследовать и изучить методы сортировки с помощью дерева.

Задача работы:

овладеть навыками написания программ для сортировки с помощью бинарного дерева на языке программирования ПАСКАЛЬ .

Порядок работы :

q       изучить описание лабораторной работы;

q       по заданию, данному преподавателем, разработать алгоритм программы решения задачи;

q       написать программу на языке ПАСКАЛЬ;

q       отладить программу;

q       решить задачу;

q       оформить отчет.

Лабораторная работа № "СПИСКОВЫЕ СТРУКТУРЫ ДАННЫХ"

Цель работы: исследовать и изучить списковые структуры данных.

Задача работы: овладеть навыками написания программ по исследованию списковых структур на языке программирования ПАСКАЛЬ .

Порядок работы :

q       изучить описание лабораторной работы;

q       по заданию, данному преподавателем, разработать алгоритм программы решения задачи;

q       написать программу на языке ПАСКАЛЬ;

q       отладить программу;

q       решить задачу;

q       оформить отчет.

Линейные однонаправленные списки

Под односвязными списками понимают упорядоченную последовательность элементов, каждый из которых имеет 2 поля : информационное поле info

и поле указателя ptr .

Особенностью указателя является то, что он дает только адрес последующего элемента списка. У однонаправленных списков поле указателя последнего элемента в списке является пустым nil.

Lst - указатель начала списка. Он представляет список как единое целое. Иногда список может быть пустым, т.е. в данном списке нет ни одного элемента. В этом случае lst = nil.

Линейный поиск

Если нет никакой дополнительной информации о разыскиваемых данных, то очевидный подход - простой последовательный просмотр массива с увеличением шаг за шагом той его части, где желаемого элемента не обнаружено. Такой метод называется линейным поиском. Условия окончания поиска таковы:

1. Элемент найден, т.е. ai = x.

2. Весь массив просмотрен и совпадения не обнаружено.

Это дает нам линейный алгоритм:

i := 0;

WHILE (i < N) AND (a[i] <> x) DO

  i := i+1 ;

END;

Обратите внимание, что порядок элементов в логическом выражении имеет существенное значение. Инвариант цикла, т.е. условие, выполняющееся перед каждым увеличением индекса i, выглядит так:

(0 £ i < N) AND (Ak : 0 £ k < i : ak ¹ x)

Он говорит, что для всех значений k, меньших чем i, совпадения не было. Отсюда и из того факта, что поиск заканчивается только в случае ложности условия в заголовке цикла, можно вывести окончательное условие:

((i = N) OR (ai = x)) AND (Ak : 0 £  k < i : ak ¹ x)

Это условие не только указывает на желаемый результат, но из него же следует, что если элемент найден, то он найден вместе с минимально возможным индексом, т.е. это первый из таких элементов. Равенство i = N свидетельствует, что совпадения не существует.

Совершенно очевидно, что окончание цикла гарантировано, поскольку на каждом шаге значение i увеличивается, и, следовательно, оно, конечно же, достигнет за конечное число шагов предела N; фактически же, если совпадения не было, это произойдет после N шагов.

Ясно, что на каждом шаге требуется увеличивать индекс и вычислять логическое выражение. А можно ли эту работу упростить и таким образом убыстрить поиск ?

Единственная возможность - попытаться упростить само логическое выражение, ведь оно состоит из двух членов. Следовательно, единственный шанс на пути к более простому решению - сформулировать простое условие, эквивалентное нашему сложному. Это можно сделать, если мы гарантируем, что совпадение всегда произойдет. Для этого достаточно в конец массива поместить дополнительный элемент со значением x. Назовем такой вспомогательный элемент "барьером", ведь он охраняет нас от перехода за пределы массива. Теперь массив будет описан так:

a: ARRAY[0..N] OF INTEGER

и алгоритм линейного поиска с барьером выглядит следующим образом:

a[N] := x;

i := 0;

WHILE a[i] <> x DO

  i := i+1;

 END;

Результирующее условие, выведенное из того же инварианта, что и прежде:

(ai=x) AND (Ak : 0 £ k < i : ak ¹ x)

Ясно, что равенство i = N свидетельствует о том, что совпадения (если не считать совпадения с барьером) не было.

Литература

1.   Бертисс А.Т.  Структуры данных./Пер.с англ.- М.:Статистика,1974.

2.   Вирт Н.  Алгоритмы и структуры данных.- М.: Мир,1989.

3.   Д. Райли. Абстракция и структуры данных. Вводный курс. М.: Мир, 1993.

4.   Костин А.Е.,Шаньгин В.Ф.  Организация и обработка структур данных в вычислительных системах.- М.: Высшая школа,1987.

5.   Ленгсам и др.

Структуры данных для персональных ЭВМ. - М.: Мир, 1989.

6.   Трамбле Ж., Соренсон П.  Введение  в  структуры данных. - М.: Машиностроение, 1982.

 

Логический тип - BOOLEAN

Стандартный логический тип Boolean (размер-1 байт) представляет собой тип данных, любой элемент которого может принимать лишь 2 значения: True и False.

Над логическими элементами данных выполняются логические операции. Основные из них:

a) Отрицание (NOT)

b) Конъюнкция (AND)

c) Дизъюнкция (OR)

Таблица истинности основных логических функций.

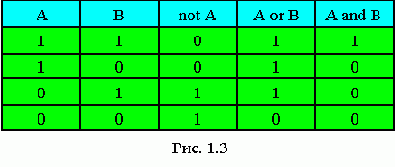
      Логические значения получаются также при реляционных операциях с целыми числами.

Массивы

В общем случае элемент массива - это есть элемент вектора, который сам по себе тоже является элементом структуры (рис. 2.6).

Для доступа к элементу двумерного массива необходимы значения пары индексов (номер строки и номер столбца, на пересечении которых находится элемент). На физическом уровне двумерный массив выглядит также, как и одномерный (вектор), причем трансляторы представляют массивы либо в виде  строк, либо в виде столбцов.

Метод исследования

Данная курсовая работа заключается в исследовании прямых методов сортировки:

- метода прямого выбора;

- метода прямого включения;

- метода прямого обмена.

Исследование заключается в следующем:

берут три массива с одинаковым количеством элементов, но один из них упорядоченный по возрастанию, второй - по убыванию, а третий - случайный. Осуществляется сортировка данных массивов и сравнивается количество перемещений элементов при сортировке первого, второго и третьего массивов, а также сравнивается количество сравнений при сортировке.

Вышеописанный способ применяется для массивов, состоящих из 10, 100, 1000 и 10000  упорядоченных и неупорядоченных элементов для всех методов сортировки.

Метод транспозиции

В данном методе найденный элемент переставляется  на  один элемент к голове списка. Если к этому элементу обращаются часто, то постепенно перемещаясь к началу списка, он скоро окажется в его голове.

Этот метод удобен тем, что он эффективен не только в  списковых структурах, но и в неупорядоченных массивах, т.к. меняются местами только два рядом стоящих элемента.

Будем использовать три указателя:

       p - рабочий указатель, указывает на элемент.

       q - вспомогательный указатель, отстает на один шаг от p.

       s -  вспомогательный указатель, отстает на два шага от p.

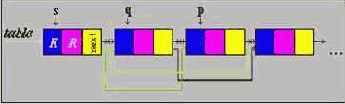
Найденный нами третий элемент передвигается на один шаг к голове списка (т.е. становится вторым). Указатель первого элемента перемещается на третий элемент, указатель второго элемента на четвертый, таким образом третий элемент перемещается на второе место. Если к данному элементу обратиться еще раз, то он окажется в голове списка.

s=nil

q=nil

p=nil

while (p<>nil) do

  if key=k(p) then search=p

  if q=nil then return

  else next(q)=next(p)

         next(p)=q

          if s=nil then table

          else next(s)=p

         end if

         search=p

  end if

  end if

  return

end while

search=nil return

В данном методе найденный элемент переставляется на один элемент к голове списка. И если к этому элементу обращаются часто, то, перемещаясь к голове списка, он скоро окажется на первом месте.

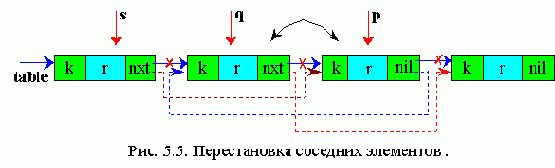
р - рабочий указатель

q - вспомогательный указатель, отстает на один шаг от р

s - вспомогательный указатель, отстает на два шага от q

Алгоритм метода транспозиции:

Псевдокод: s=nil q=nil p=table while (p <> nil) do   if key = k(p) then     ‘ нашли, транспонируем     if q = nil then        ‘ переставлять не надо        search=p        return     endif     nxt(q)=nxt(p)     nxt(p)=q     if s = nil then       table = p       else nxt(s)=p     endif     search=p     return   endif endwhile search=nil return

Паскаль: s:=nil; q:=nil; p:=table; while (p <> nil) do   begin     if key = p^.k then       ‘ нашли, транспонируем       begin                if q = nil then             begin             ‘переставлять не на-               до  search:=p;             exit;           end;           q^.nxt:=p^.nxt;           p^.nxt:=q;           if s = nil then             table := p;           else              begin                  s^.nxt := p;           end;           search:=p;           exit;   end; end; search:=nil; exit;

Этот метод удобен при поиске не только в списках, но и в массивах (так как меняются только два стоящих рядом элемента).

Методическое руководство к курсовой работе

Введение

 

Курсовая работа выполняется студентами специальности 22.04 в четвертом семестре.

Целью курсовой работы является закрепление основ и углубление знаний в области структур и алгоритмов обработки данных в ЭВМ.

Тематика заданий на курсовую работу, приведенных в данных методических указаниях, может быть дополнена, расширена, увязана с решением актуальных научно-исследовательских задач, выполняемых на кафедре.

Методы оптимизации поиска

Всегда можно говорить о некотором значении вероятности поиска того или иного элемента в таблице. Считаем, что в таблице данный элемент существует. Тогда вся таблица поиска может быть представлена как система с дискретными состояниями, а вероятность нахождения там искомого элемента - это вероятность p(i) i - го состояния системы.

 Количество сравнений при поиске в таблице, представленной как дискретная система, представляет собой математическое ожидание значения дискретной случайной величины, определяемой вероятностями состояний и номерами состояний системы.

Z=Q=1p(1)+2p(2)+3p(3)+…+np(n)

Желательно, чтобы p(1)?p(2) ?p(3) ?…?p(n).

Это минимизирует количество сравнений, то есть увеличивает эффективность. Так как последовательный поиск начинается с первого элемента, то на это место надо поставить элемент, к которому чаще всего обращаются (с наибольшей вероятностью поиска).

Наиболее часто используются два основных способа автономного переупорядочивания таблиц поиска. Рассмотрим их на примере односвязных списков.

Нелинейные связанные структуры

Двусвязный список может быть нелинейной структурой данных, если вторые указатели задают произвольный порядок следования элементов (рис.3.13).

LST1 - указатель на начало 1 - ого списка (ориентированного указателем P1). Он линейный и состоит из 5-и элементов.

2-ой список образован из этих же самых элементов, но в произвольной последовательности. Началом 2-ого списка является 3-ий элемент, а концом 2-ой элемент.

В общем случае элемент списочной структуры может содержать сколь угодно много указателей, то есть может указывать на любое количество элементов.

Можно выделить 3 признака отличия нелинейной структуры:

      1)  Любой элемент структуры может ссылаться на любое число других элементов структуры, то есть может иметь любое число полей-указателей.

          2)  На данный элемент структуры может ссылаться любое число других элементов этой структуры.

          3)  Ссылки могут иметь вес, то есть подразумевается иерархия ссылок.

Представим, что имеется дискретная система, в графе состояния которой узлы - это состояния, а ребра - переходы из состояния в состояние (рис. 3.14).

     Входной сигнал в систему это X. Реакцией на входной сигнал является выработка выходного сигнала Y и переход в соответствующее состояние.

Граф состояния дискретной системы можно представит в виде двусвязного нелинейного списка. При этом в информационных полях должна записываться информация о состояниях системы и ребрах. Указатели элементов должны формировать логические ребра системы (рис. 3.15).

Для реализации вышесказанного:

1) должен быть создан список, отображающий состояния системы       (1, 2, 3);

2) должны быть созданы списки, отображающие переходы по ребрам из соответствующих состояний .

В общем случае при реализации многосвязной структуры получается сеть.

 

 

Контрольные вопросы

        1.        Какие динамические структуры Вам известны?

        2.        В чем отличительная особенность динамических объектов?

        3.        Какой тип представлен для работы с динамическими объектами?

        4.        Как связаны элементы в динамической структуре ?

        5.        Назовите основные особенности односвязного списка..

        6.        В чем отличие линейных списков от кольцевых ?

        7.        Зачем были введены двусвязные списки ?

        8.        В чем разница в операциях, производимых над односвязными и двусвязными списками ?

        9.        Какой список является более удобным в обращении, односвязный или двусвязный ?

     10.     Что такое указатель?

     11.     Какие стековые операции можно производить над списками ?

     12.     Какие операции, производимые над очередью, можно производить над списками ?

     13.     Почему можно производить все эти операции над списками ?

     14.     Для чего предназначены операции Getnode и Freenode?

     15.     Какие методы утилизации вы знаете ?

     16.     Перечислите элементы заголовков в списках.

     17.     Зависит ли время, затраченное на вставку элемента в односвязный список, от количества элементов в списке ?

     18.     Где процесс вставки и удаления эффективнее, в списке или в массиве ?

     19.     Как можно производить просмотр односвязного списка?

     20.     Что означает AVAIL?

     21.     Какой недостаток односвязных списков по сравнению с

     22.     массивом?

     23.     Какие структуры являются нелинейными ?

     24.     Каковы признаки отличия нелинейных структур?

     25.     Как можно создать нелинейную связную структуру?

     26.     Что такое граф состояния ?

Обход дерева слева - направо

  procedure InTree(tree);

   begin

       if Tree = nil then write('Дерево пусто')

       else

           with Tree^ do

             begin

                if left<>nil then InTree(left);

                if right<>nil then InTree(right); 

             end;

 end;

Очередь

Понятие очереди всем хорошо известно из повседневной жизни. Элементами очереди в общем случае являются заказы на то или иное обслуживание.

В программировании имеется структура данных, которая называется очередью. Эта структура данных используется, например, для моделирования реальных очередей с целью определения их характеристик при данном законе поступления заказов и дисциплине их обслуживания. По своему существу очередь является полустатической структурой- с течением времени и длина очереди, и состав могут изменяться.

На рис. 2. 13  приведена  очередь,  содержащая четыре элемента — А, В, С и D. Элемент А расположен в начале очереди, а элемент D — в ее конце. Элементы могут удаляться только из начала очереди, то есть первый помещаемый в очередь элемент удаляется первым. По этой причине очередь часто называют списком, организованным по принципу «первый размещенный первым удаляется» в противоположность принципу стековой организации — «последний размещенный первым удаляется».

Дисциплину обслуживания, в которой заказ, поступивший в очередь первым, выбирается первым для обслуживания (и удаляется из очереди), называется FIFO (First In First Out - Первым пришел, первым ушел). Очередь открыта с обеих сторон.

Таким образом, изъятие компонент происходит из начала очереди, а запись- в конец. В этом случае вводят два указателя: один - на начало очереди, второй- на ее конец.

Реальная очередь создается в памяти ЭВМ в виде одномерного массива с конечным числом элементов, при этом необходимо указать тип элементов очереди, а также необходима переменная в работе с очередью.

Физически очередь занимает сплошную область памяти и элементы следуют друг за другом, как в последовательном списке.

Операции, производимые над очередью:

Для очереди определены три примитивные операции. Операция insert (q,x) помещает элемент х в конец очереди q. Операция remove(q) удаляет элемент из начала очереди q и присваивает его значение переменной х. Третья операция, empty (q), возвращает значение true или false в зависимости от того, является ли данная очередь пустой или нет.
Кроме того. Учитывая то, что полустатическая очередь реализуется на одномерном массиве, необходимо следить за возможностью его переполнения. Сэтой целью вводится опнрация full(q).

Операция insert может быть выполнена всегда, поскольку на количество элементов, которые может содержать очередь, никаких ограничений не накладывается. Операция remove, однако, применима только к непустой очереди, поскольку невозможно удалить элемент из очереди, не содержащей элементов. Результатом попытки удалить элемент из пустой очереди является возникновение исключительной ситуации

потеря значимости. Операция empty, разумеется, выполнима всегда.

 

Пример реализации очереди в виде одномерного массива на Паскале:

const

  MaxQ = ...

type

  E = ...

  Queue = Array [1..MaxQ] of E;

var

  Q: Queue;

  F, R: Integer;

{Указатель F указывает на начало очереди. Указатель R указывает на конец очереди.     Если очередь пуста, то F = 1, а R = 0 (То есть R < F – условие пустоты очереди).}

Procedure Insert(I: Integer; var Q: Queue);

begin

  Inc(R);

  Q[R]:=I;

end;

Function Empty(Q: Queue): Boolean;

begin

  If R < F then Empty:=True Else Empty:=False;

end;

Procedure Remove(var I: Integer; Q: Queue);

begin

  If Not Empty(Q) then

    begin

      I:=Q[F];

      Inc(F);

    end;

end;

Пример работы с очередью с использованием стандартных процедур.

MaxQ = 5

Производим вставку элементов A, B  и C  в очередь.

Insert(q, A);

Insert(q, B);

Insert(q, C);



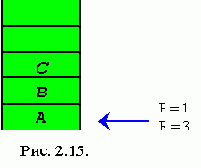
Убираем элементы A и B из очереди.

Remove(q);

Remove(q);



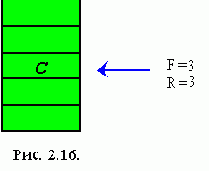
К сожалению, при подобном представлении очереди, возможно возникновение абсурдной ситуации, при которой очередь является пустой, однако новый элемент разместить в ней нельзя (рассмотрите последовательность операций удаления и вставки, приводящую к такой ситуации). Ясно, что реализация очереди при помощи массива является неприемлемой.

Одним из решений возникшей проблемы может быть модификация операции remove таким образом, что при удалении очередного элемента вся очередь смещается к началу массива.


Операция remove (q) может быть в этом случае реализована следующим образом.

X = q[1]

For I =1 to R-1

q[I] =q[I+1]

next I

R =R-1

Переменная F больше не требуется, поскольку первый элемент массива всегда является началом очереди. Пустая очередь представлена очередью, для которой значение R равно нулю.

Однако этот метод весьма непроизводителен. Каждое уда­ление требует перемещения всех оставшихся в очереди элементов. Если очередь содержит 500 или 1000 элементов, то очевидно, что это весьма неэффективный способ. Далее, операция удаления элемента из очереди логически предполагает манипулирование только с одним элементом, т. е. с тем, который расположен в начале очереди. Реализация данной операции должна отражать именно этот факт, не производя при этом множества дополнительных действий.

Другой способ предполагает рассматривать массив, который содержит очередь в виде замкнутого кольца, а не линейной последовательности, имеющей начало и конец. Это означает, что первый элемент очереди следует сразу же за последним. Это означает, что даже в том случае, если последний элемент занят, новое значение может быть размещено сразу же за ним на месте первого элемента, если этот первый элемент пуст.

Организация кольцевой очереди.



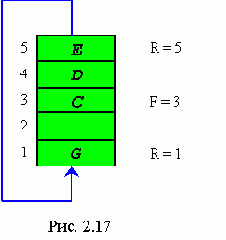
Рассмотрим пример. Предположим, что очередь содержит три элемента - в позициях 3, 4 и 5 пятиэлементного массива. Этот случай, показанный на рис. 2.17. Хотя массив и не заполнен, последний элемент очереди занят.

Если теперь делается попытка поместить в очередь элемент G, то он будет записан в первую позицию массива, как это показано на рис. 2.17. Первый элемент очереди есть Q(3), за которым следуют элементы Q (4), Q(5) и Q(l).

К сожалению, при таком представлении довольно трудно определить, когда очередь пуста. Условие R<F больше не годится для такой проверки, поскольку на рис. 2. 17 показан случай, при котором данное условие выполняется, но очередь при этом не является пустой.

Одним из способов решения этой проблемы является введение соглашения, при котором значение F есть индекс элемента массива, немедленно предшествующего первому элементу очереди, а не индексу самого первого элемента.


В этом случае, поскольку R содержит индекс последнего элемента очереди, условие F = R подразумевает, что очередь пуста.

Отметим, что перед началом работы с очередью, в F и R устанавливается значение последнего индекса массива, а не 0 и 1, поскольку при таком представлении очереди последний элемент массива немедлен­но предшествует первому элементу. Поскольку R = F, то очередь изначально пуста.

Основные операции с кольцевой очередью:

1. Вставка элемента q в очередь x.

Insert(q,x)

2. Извлечение элемента из очереди x.

Remove(q)

3. Проверка очереди на пустоту.

Empty(q)

Операция empty (q) может быть записана следующим образом:

if F = R

then empty = true

else empty = false

endif

return

Операция remove (q) может быть записана следующим образом:

empty (q)

if empty = true

then print «выборка из пустой очереди»

stop

endif

if F =maxQ

then F =1

else F = F+1

endif

x = q(F)

return

Отметим, что значение F должно быть модифицировано до момента извлечения элемента.

Операция вставки insert (q,x).

Для того чтобы запрограммировать операцию вставки, должна быть проанализирована ситуация, при которой возникает переполнение. Переполнение происходит в том случае, если весь массив уже занят элементами очереди и при этом делается попытка разместить в ней еще один элемент. Рассмотрим, например, очередь на рис. 2. 17. В ней находятся три элемента — С, D и Е, соответственно расположенные в Q (3), Q (4) и Q (5). Поскольку последний элемент в очереди занимает позицию Q (5), значение R равно 5. Так как первый элемент в очереди находится в Q (3), значение F равно 2. На рис. 2. 17 в очередь помещается элемент G, что приводит к соответствующему изменению значения R. Если произвести следующую вставку, то массив становится целиком заполненным, и попытка произвести еще одну вставку приводит к переполнению. Это регистрируется тем фактом, что F = R, а это как раз и указывает на переполнение. Очевидно, что при такой реализации нет возможности сделать различие между пустой и заполненной очередью Разумеется, такая ситуация удовлетворить нас не может

Одно из решений состоит в том, чтобы пожертвовать одним элементом массива и позволить очереди расти до объема на единицу меньшего максимального. Так, если  массив из 100 элементов объявлен как очередь, то очередь может содержать до 99 элементов. Попытка разместить в очереди 100-й элемент приведет к переполнению. Подпрограмма insert может быть записана следующим образом:

if R = max(q)

then R = 1

else R = R+1

endif

'проверка на переполнение

if R = F

then print «переполнение очереди»

stop

        endif

q (r) =x

return

Проверка на переполнение в подпрограмме insert производится после установления нового значения для R, в то время как проверка на потерю значимости в подпрограмме remove производится сразу же после входа в подпрограмму до момента обновления значения F.

Односвязные списки

Элемент односвязного списка содержит два поля (рис. 3.2): информационное поле (INFO) и поле указателя (PTR).

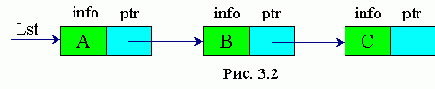
Особенностью указателя является то, что он дает только адрес последующего элемента списка. Поле указателя последнего элемента в списке является пустым (NIL). LST - указатель на начало списка. Список может быть пустым, тогда LST будет равен NIL.

Доступ к элементу списка осуществляется только от его начала, то есть обратной связи в этом списке нет.

Односвязный список, как самостоятельная структура данных

Просмотр односвязного списка может производиться только последовательно, начиная с головы (с начала) списка. Если необходимо просмотреть предыдущий элемент, то надо снова возвращаться к началу списка. Это - недостаток односвязных списков по сравнению со статическими структурами типа массива. Списковая структура проявляет свои достоинства, когда число элементов списка велико, а вставку или удаление необходимо произвести внутри списка.

Пример:

Необходимо вставить в существующий массив элемент X между 5 и 6 элементами.

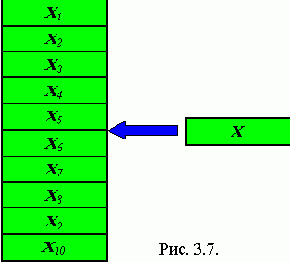
Для проведения данной операции в массиве нужно “опустить” все элементы, начиная с X6 - увеличить их индексы на единицу. В результате вставки получаем следующий массив (рис. 3.7, 3.8):

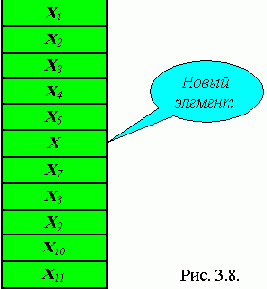
Данная процедура может занимать очень значительное время. В противоположность этому, в связанном списке операция вставки состоит в изменении значения 2-х указателей и генерации свободного элемента. Причём время, затраченное на выполнение этой операции, является постоянным и не зависит от количества элементов в списке.

Операция FreeNode

При освобождении элемента Nod(P) из функционального списка операцией FreeNode(P), он заносится в свободный список.

Ptr(P) = Avail

Avail = P

Операция GetNode

Разработаем процедуру, которая будет создавать пустой элемент списка с указателем Р.

Для реализации операции GetNode необходимо указателю сгенерированного элемента присвоить значение указателя начала свободного списка, а указатель начала перенести к следующему элементу.

P = Avail

Avail = Ptr(Avail)

Перед этим надо проверить, есть ли элементы в списке. Пустота свободного списка (Avail = Nil), эквивалентна переполнению функционального списка. 

If Avail = Nil then Print “Переполнение”  Stop

Else

  P = Avail

  Avail = Ptr(Avail)

Endif

 

Описание процедур, используемых в программе

UPOR		процедура генерирует упорядоченный по возрастанию массив чисел
NOTUPOR		процедура генерирует неупорядоченный (случайный) массив чисел
PR_CHOOSE		процедура осуществляет сортировку методом прямого выбора
PR_INS		процедура осуществляет сортировку методом прямой  вставки
PR_OBM		процедура осуществляет сортировку методом прямого обмена
MAKE		процедура осуществляет исследование прямых методов сортировки
EXAMPLE		процедура выполняет контрольный пример (сортировку методом прямого включения)

Текст программы

 

{$M 65000,65000,65000}

{Выделение памяти осуществляется для того, чтобы было возможно осуществлять исследование  массива, содержащего 10000 элементов

***********************************************************

        Данная программа является курсовой работой по дисциплине

               'Структуры и алгоритмы обработки данных'

                  на тему 'Прямые методы сортировки'

                   В работе исследуются методы:

                          - прямого выбора;

                          - прямого обмена;

                          - прямой вставки.

   Для исследования используются массивы из 10,100,100,10000 элементов.

**********************************************************}

{ использование модулей для осуществления вывода на экран }

uses crt,crtext,dcrt;***************************************************}

{** процедура, генерирующая упорядоченный по возрастанию массив чисел**}

{*********************************************************}

procedure upor(a:array of integer;var a1:array of integer);

var

{i - счетчик в циклах}

 i:integer;

begin

{первый элемент принимает значение 1}

a[0]:=1;

 for i:=1 to high(a) do

  begin

{каждый последующий элемент принимает значение,

равное значению предыдущего элемента + случайное число}

   a[i]:=a[i-1]+random(2);

  end;

 for i:=0 to high(a) do

   a1[i]:=a[i];

end;

{*********************************************************}

{** процедура, генерирующая  не упорядоченный (случайный) массив чисел**}

{*********************************************************}
procedure notupor(a:array of integer;var a1:array of integer);
var
{i - счетчик в циклах}
 i:integer;
begin
 for i:=0 to high(a) do
  begin { элемент массива принимает случайное значение из диапазона 0 <= a[i] < 9999}
   a[i]:=random(9999);
  end;
 for i:=0 to high(a) do
   a1[i]:=a[i];
end;
{*********************************************************}
{***** процедура, осуществляющая сортировку методом прямого выбора***}
{*********************************************************}
procedure pr_choose(a:array of integer;var a1:array of integer;var k,k1:longint);
var
{i,j - счетчики в циклах}
 i,j:integer;
{x - переменная для осуществления обмена между a[i] и a[j]}
 x:integer;
begin
{k1  -  переменная для подсчета количества сравнений
 k   -  переменная для подсчета количества перемещений}
           k:=0;k1:=0;
{high(a) - функция, возвращающая номер последнего элемента массива}
for i := 0 to high(a) - 1 do
  begin
    for j := i + 1 to high(a) do
     begin
      k1:=k1+1;
      if a[i] < a[j] then
        begin
         k:=k+1;
  {перестановка i-го с j-м элементом с помощью переменной x}
          x:=a[i];
          a[i]:=a[j];
          a[j]:=x;
        end;
     end;
  end;
for i:=0 to high(a) do
 a1[i]:=a[i];
end;
{**********************************************************
 ***** процедура, осуществляющая сортировку методом прямого *
 *************** обмена(метод пузырька) *********************
**********************************************************}
procedure pr_obm(a:array of integer;var a1:array of integer;var k,k1:longint);
var
{i,j - счетчики в циклах}
 i,j:integer;
{x - переменная для осуществления обмена между a[j-1] и a[j]}
 x:integer;
begin
{k1 -  переменная для подсчета количества сравнений
 k  -  переменная для подсчета количества перемещений}
k:=0;k1:=0;
for i := 1 to high(a) do
 begin
  for j := high(a) downto i do
   begin


    k1:=k1+1;
    if a[j - 1] < a[j] then
      begin
        k:=k+1;
  {обмена содержимым элементов массива a[j-1] и a[j]
   с помощью переменной x}
        x := a[j - 1];
        a[j - 1] := a[j];
        a[j] := x;
      end;
    end;
 end;
 for i:=1 to high(a) do
  a1[i]:=a[i];
end;
{*********************************************************}
{*** процедура, осуществляющая сортировку методом прямого включения **}
{*********************************************************}
procedure pr_ins(a:array of integer;var a1:array of integer;var k,k1:longint);
var
{i,j - счетчики в циклах}
 i,j:integer;
{x - переменная для осуществления обмена между a[i] и a[j]}
 x:integer;
begin
{k1 -  переменная для подсчета количества сравнений
 k  -  переменная для подсчета количества перемещений}
k:=0;k1:=0;
for i := 1 to high(a) do
  begin
    x := a[i];
    for j := i - 1 downto 0 do
     begin
      k1:=k1+1;
      if x > a[j] then
                    begin
                     k:=k+1;
  {обмена содержимым элементов массива a[j+1] и a[j]
   с помощью переменной x}
                     a[j + 1] := a[j];
                     a[j]:=x;
                    end;
     end;
  end;
  for i:=0 to high(a) do
   a1[i]:=a[i];
end;
{**********************************************************
        процедура, осуществляющая исследование методов сортировок  для
 ***********  заданного массива чисел  ***********************
**********************************************************}
procedure make(x1,n:integer;a,a1:array of integer;k:byte);
var
{количество перестановок}
 kol_pr_ins, kol_pr_obm,kol_pr_choose:longint;
{количество сравнений}
 kol_sr_ins, kol_sr_obm,kol_sr_choose:longint;
  s:string;
begin
case k of
1:s:='упорядоченных по возрастанию';
2:s:='неупорядоченных (случайных)';
3:s:='упорядоченных по убыванию';
end;
{--------метод прямого включения---------}
pr_ins(a,a1,kol_pr_ins,kol_sr_ins);
{--------метод прямого обмена (метод пузырька)--------}


pr_obm(a,a1,kol_pr_obm,kol_sr_obm);
{---------метод прямого выбора----------}
pr_choose(a,a1,kol_pr_choose,kol_sr_choose);
{** вывод результата исследования **}
{вывод шапки таблицы}
gotoxy(3,x1);textcolor(cyan);textbackground(1);
writeln('Для ',high(a)+1,' ',s,' элементов:');
gotoxy(3,x1+1);textcolor(lightgreen);textbackground(1);
writeln('Методы:    прямого включения    прямого обмена     прямого выбора');
{вывод полученных при исследовании данных}
gotoxy(3,x1+2);textcolor(white);write('перест.');
gotoxy(17,wherey);write(kol_pr_ins);
gotoxy(37,wherey);write(kol_pr_obm);
gotoxy(58,wherey);writeln(kol_pr_choose);
gotoxy(3,x1+3);write('сравн.');
gotoxy(17,wherey);write(kol_sr_ins);
gotoxy(37,wherey);write(kol_sr_obm);
gotoxy(58,wherey);writeln(kol_sr_choose);
str(high(a)+1,s);box(1,19,80,24,1,15,double,s+' элементов');
 gotoxy(4,20);write('Сортировка ',s,' элементов по убыванию');
 gotoxy(4,21);write('Сортируются ',s,' упорядоченных(по возрастанию) элементов');
 gotoxy(4,22);write('Сортируются ',s,' неупорядоченных(случайных) элементов');
 textbackground(lightgray);
 textcolor(red);gotoxy(3,25);write('Esc - главное меню');
end;
{*********************************************
  Пример сортировки методом прямого включения
 Дан массив записей, содержащий:
           -имя студента;
           -кол-во баллов (рейтинг).
   Необходимо отсортировать данный массив по
   убыванию  количества  баллов  у  студента.
*********************************************}
procedure example;
type
{rec - запись, содержащая:
                 name - имя студента;
                 num  - кол-во баллов (рейтинг).}
 rec=record
      name:string;
      num:byte;
     end;
var
{mas - массив записей rec}
 mas:array[1..20] of rec;
{счетчики в циклах}
 i,j:integer;
 x:rec;
{переменные для подсчета количества сравнений и перемещений
 во время сортировки}
 k_sr,k_p:integer;
 key:char;
begin
{переменные для подсчета количества сравнений и перемещений
 во время сортировки}


 k_sr:=0;k_p:=0;
randomize;
{Данный массив, содержащий имена студентов}
mas[1].name:='Иван';mas[2].name:='Петр';mas[3].name:='Сидор';
mas[4].name:='Василий';mas[5].name:='Денис';mas[6].name:='Геннадий';
mas[7].name:='Борис';mas[8].name:='Марат';mas[9].name:='Казбек';
mas[10].name:='Алексей';mas[11].name:='Владимир';mas[12].name:='Сидор';
mas[13].name:='Виталий';mas[14].name:='Александр';mas[15].name:='Михаил';
mas[16].name:='Евгений';mas[17].name:='Артур';mas[18].name:='Руслан';
mas[19].name:='Мурат';mas[20].name:='Аркадий';
{задание количества баллов у студента случайным образом}
for i:=1 to 20 do
 mas[i].num:=random(19)+1;
{вывод пояснений}
getshadow;
textbackground(lightgray);
textcolor(red);gotoxy(15,1);write(' Пример сортировки по убыванию методом прямого включения');
textbackground(lightgray);
textcolor(red); gotoxy(3,25);  write('Esc - главное меню');
textcolor(red); gotoxy(65,25); write('F1 - задание');
box(58,0,80,25,1,15,double,'Статистика');
textcolor(lightmagenta);
gotoxy(59,3); write(' Сортировка  методом ');
gotoxy(61,4); write('прямого включения.');
textcolor(white); gotoxy(59,5); write('---------------------');
box(31,0,57,25,1,15,double,'После сортировки');
textcolor(lightmagenta); gotoxy(32,3); write(' N   Имя           балл');
box(1,0,30,25,1,15,double,'До сортировки');
textcolor(lightmagenta); gotoxy(3,3);  write('N   Имя              балл');
{вывод на экран исходного массива}
for i:=1 to 20 do
 begin
textcolor(lightcyan); gotoxy(3,i+3);  write(i);
textcolor(yellow);    gotoxy(7,i+3);  write(mas[i].name);
textcolor(lightred);  gotoxy(25,i+3); writeln(mas[i].num);
 end;
{сортировка по убыванию количества баллов}
for i := 2 to 20 do
  begin
    x := mas[i];
    for j := i - 1 downto 1 do
     begin
  {k_sr - счетчик количества сравнений}
    k_sr:= k_sr+1;
          if x.num > mas[j].num then
                    begin
  {k_p - счетчик количества перемещений}
                    k_p:=k_p+1;
  {обмена содержимым элементов массива mas[j+1] и mas[j]


   с помощью переменной x}
                     mas[j + 1] := mas[j];
                    mas[j]:=x;
                    end;
     end;
  end;
{вывод на экран отсортированного массива}
for i:=1 to 20 do
 begin
textcolor(lightcyan); gotoxy(33,i+3);  write(i);
textcolor(yellow);    gotoxy(37,i+3);  write(mas[i].name);
textcolor(lightred);  gotoxy(52,i+3);  writeln(mas[i].num);
 end;
{ вывод на экран количества сравнений и перестановок
 в массиве, осуществленных во время сортировки}
 textcolor(lightgreen); gotoxy(61,6); write('Сравнений:');
 textcolor(lightgray);  gotoxy(75,6); write(k_sr);
 textcolor(lightgreen); gotoxy(61,8); write('Перестановок:');
 textcolor(lightgray);  gotoxy(75,8); write(k_p);
   repeat
   key:=' ';   if keypressed then  key:=readkey;
    case key of
    {#59 - код клавиши F1}
    #59:begin
    {вывод окна с заданием для контрольного примера}
    {putshadow+box - вывод окна с тенью}
     putshadow(15,7,65,15);box(15,7,65,15,lightgray,0,double,'Задание');
         textcolor(red);
         gotoxy(21,9);  write('Дан список, содержащий фамилии студентов');
         gotoxy(21,10); write('и их рейтинговые  баллы. Необходимо от-');
         gotoxy(21,11); write('сортировать данный список  по убыванию ');
         gotoxy(21,12); write('рейтинговых баллов.');
         textcolor(yellow);gotoxy(50,15);write('Enter - отмена');
        end;
    {#13 - код клавиши Enter}
    #13:getshadow;
    end;
    {#27 - код клавиши Esc}
   until key=#27;
end;
{**********************************************************
************************  Основная программа **************
**********************************************************}
const
{массив строк - пунктов главного меню}
 menu:array[1..7] of string=(' Пример сортировки  ',' Исследование (10 эл-тов)',
                             ' Исследование (100 эл-тов) ',
                             ' Исследование (1000 эл-тов) ',
                             ' Исследование (10000 эл-тов)  ',


                             ' О программе '
                             ,' Выход ');
var
{массивы чисел, используемые для исследования}
 a,a1:array[0..9] of integer;    {10    - чисел}
 b,b1:array[0..99] of integer;   {100   - чисел}
 c,c1:array[0..999] of integer;  {1000  - чисел}
 d,d1:array[0..9999] of integer; {10000 - чисел}
 f:byte;                         {показатель того , какой массив
                                  поступает в процедуру для упо-
                                  рядочивания по убыванию:
                                   1     - неупорядоченный (слу-
                                           чайный);
                                   2     - упорядоченный по воз-
                                           растанию;
                                   3     - упорядоченный по убы-
                                           ванию}.
 k:char;
 item:byte;
begin
clrscr;cursoroff; {гашение курсора}
repeat
textbackground(0);clrscr;
{fill - процедура, заполняющая заданную область  экрана заданными  символами заданного  цвета}
fill(lightgray,1,1,2,80,25,' ');
{menuv - процедура, выводящая на экран вертикальное меню}
menuv(25,10,menu,lightgray,black,red,lightgreen,yellow,'Сортировка',item,double);
{item - переменная, содержащая номер выбранного пункта меню}
case item of
1:example;
2:begin
       {getshadow - процедура, убирающая тень от меню}
          getshadow;
       {** исследуются 10 упорядоченных по возрастанию элементов **}
       {box - процедура, выводящая на экран окно}
           box(1,0,80,18,1,15,double,'10 элементов');
       {вызов процедуры upor, генерирующей упорядоченный по возрастанию
        массив чисел}
           upor(a,a);
       {вызов процедуры make, осуществляющей исследование методов сортировки}
           make(3,10,a,a1,1);
       {** исследуются 10 неупорядоченных (случайных) элементов **}
       {вызов процедуры notupor, генерирующей неупорядоченный(случайный)  массив чисел}


          notupor(a,a);
       { вызов процедуры make, осуществляющей исследование методов сортировки}
          make(8,10,a,a1,2);
       {** исследуются 10 упорядоченных по убыванию элементов **}
       {вызов процедуры make, осуществляющей исследование методов сортировки}
          make(13,10,a1,a1,3);
       {ожидание нажатия клавиши Esc}
     repeat
      k:=readkey;
     until k=#27;
  end;
3:begin
       {getshadow - процедура, убирающая тень от меню}
       getshadow;
       {box - процедура, выводящая на экран окно}
       box(1,0,80,18,1,15,double,'100 элементов');
      {исследуются 100 упорядоченных по возрастанию элементов}
         upor(b,b);
         make(3,100,b,b1,1);
      {исследуются 100 неупорядоченных (случайных) элементов}
          notupor(b,b);
          make(8,100,b,b1,2);
       {исследуются 100 упорядоченных по убыванию элементов}
          make(13,100,b1,b1,3);
     repeat   k:=readkey;    until k=#27;
  end;
4:begin
       {getshadow - процедура, убирающая тень от меню}
       getshadow;
       box(1,0,80,18,1,15,double,'1000 элементов');
 {исследуется 1000 упорядоченных по возрастанию элементов}
   upor(c,c);
   make(3,1000,c,c1,1);
 {исследуется 1000 неупорядоченных (случайных) элементов}
   notupor(c,c);
   make(8,1000,c,c1,2);
 {исследуется 1000 упорядоченных по убыванию элементов}
   make(13,1000,c1,c,3);
     repeat
      k:=readkey;
     until k=#27;
  end;
5:begin
       getshadow;
       box(1,0,80,18,1,15,double,'10000 элементов');
 {исследуются 10000 упорядоченных по возрастанию элементов}
   upor(d,d);
   make(3,10000,d,d1,1);
 {исследуются 10000 неупорядоченных (случайных) элементов}
   notupor(d,d);
   make(8,10000,d,d1,2);
  {исследуются 10000 упорядоченных по убыванию элементов}
   make(13,10000,d1,d,3);
     repeat
      k:=readkey;
     until k=#27;
  end;
6:begin
       {getshadow - процедура, убирающая тень от меню}
       getshadow;
       {ввод окна с темой курсовой работы}
       box(10,5,70,15,lightgray,0,double,'О программе');
       putshadow(10,5,70,15);
       textcolor(brown);
       gotoxy(12,7);write('Данная программа является курсовой работой по дисциплине');
       gotoxy(21,8);write('"Алгоритмы и структуры обработки данных"');
       gotoxy(30,9);write('Тема курсовой работы: ');
       gotoxy(18,10);write('   "Исследование прямых методов сортировки"');
       gotoxy(17,11);write('Курсовую работу выполнили студенты группы 95-ОА-21');
         textcolor(red);gotoxy(3,25);write('Esc - главное меню');
     repeat
      k:=readkey;
     until k=#27;
  end;
end;
until item=7;
end.
{*********************конец программы********************}
 

Организация операций Getnode, Freenode и утилизация освободившихся элементов

 

Для более эффективного использования памяти компьютера (для исключения мусора, то есть неиспользуемых элементов) при работе его со списками создается свободный список, имеющий тот же формат полей, что и у функциональных списков.

Если у функциональных списков разный формат, то надо создавать свободный список каждого функционального списка.

Количество элементов в свободном списке должно быть определено задачей, которую решает программа. Как правило, свободный список создается в памяти машины как стек. При этом создание (GetNode) нового элемента  эквивалентно выборке элемента свободного стека, а операция FreeNode  - добавлению в свободный стек освободившегося элемента.

Пусть нам необходимо создать пустой список по типу стека (рис. 3.6) с указателем начала списка - AVAIL. Разработаем процедуры, которые позволят нам создавать пустой элемент списка и освобождать элемент из списка. 

Организационно-методические указания

1.   Перед началом лабораторной работы проводится консультация по методике выполнения лабораторных работ по данной дисциплине.

2.   Объем каждой лабораторной работы, подготовка и порядок выполнения построены таким образом, чтобы все студенты выполнили работу и сдали отчеты.

3.   Студенты готовятся к выполнению очередной работы заблаговременно.

4.   Студенты обязаны изучить технику безопасности при работе на лабораторных установках до 1000 В.

5.   Готовясь к лабораторному занятию, студент обязан изучить необходимый теоретический материал, пользуясь настоящими указаниями и рекомендованной литературой, произвести необходимые расчеты, заполнить соответствующую часть отчета и дать ответы на контрольные вопросы.

6.   Неподготовленные студенты к выполнению лабораторной работы не допускаются.

7.   Студенты, не сдавшие отчет во время занятия, сдают его в назначенное преподавателем время.

8.   Студент, не выполнивший лабораторную работу, выполняет ее в согласованное с преподавателем время.

9.   Каждая лабораторная работа выполняется студентами самостоятельно. Все студенты предъявляют индивидуальные отчеты. Допускается предъявление отчета в виде электронного документа.

10.         Проверка знаний студентов производится преподавателем во время лабораторного занятия и при сдаче отчета.

11.         При сдаче отчета студент должен показать знание теоретического материала в объеме, определяемом контрольными вопросами, а также пониманием физической сущности выполняемой работы.

Основные операции с деревьями

1. Обход дерева.

2. Удаление поддерева.

3. Вставка поддерева.

 

Для выполнения обхода дерева необходимо выполнить три процедуры:

1.Обработка корня.

2.Обработка левой ветви.

3.Обработка правой ветви.

 

В зависимости от того, в какой последовательности выполняются эти три процедуры, различают три вида обхода.

1.Обход сверху вниз. Процедуры выполняются в последовательности

1- 2 - 3.

2.Обход слева направо. Процедуры выполняются в последовательности

2 - 1- 3.

3.Обход снизу вверх. Процедуры выполняются в последовательности

2 - 3 -1.

В зависимости от того, какой по счету заход в узел приводит к обработке узла, получается реализация одного из трех видов обхода. Если обработка идет после первого захода в узел, то сверху вниз, если после второго, то слева направо, если после третьего, то снизу вверх (см. рис. 4. 7).

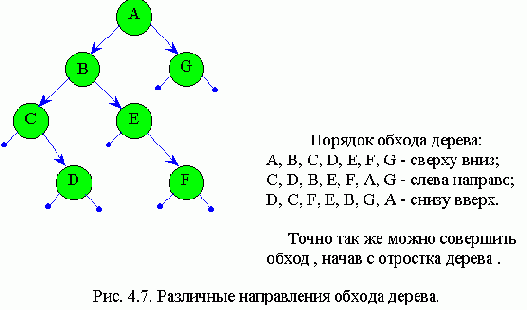
Операция исключения поддерева. Необходимо указать узел, к которому подсоединяется исключаемое поддерево и индекс этого поддерева. Исключение поддерева состоит в том, что разрывается связь с исключаемым поддеревом, т. е. указатель элемента устанавливается в nil, а степень исхода данного узла уменьшается на единицу.

Вставка поддерева - операция, обратная исключению. Надо знать индекс включаемого поддерева, узел, к которому подвешивается дерево, установить указатель этого узла на корень поддерева, а степень исхода данного узла увеличивается на единицу. При этом в общем случае необходимо произвести перенумерацию сыновей узла, к которому подвешивается поддерево.

Алгоритм  вставки и удаления  рассмотрен  в  главе 5.

---

---