Односторонние машины Тьюринга

Машина Тьюринга

называется односторонней, если в процессе вычисления ее головка никогда не сдвигается левее начальной ячейки (т.е. всегда находится в ячейках с положительными номерами).

Лемма 9.2. Для всякой м.Т.

можно построить эквивалентную одностороннюю м.Т. .

Доказательство. Пусть

Будем считать (используя лемму 1 ), что завершает работу в стандартных конфигурациях. Требуемая м.Т. будет моделировать работу , используя "многоэтажную" ленту . Содержимое ячеек на 1-ом (нижнем) этаже будет на каждом такте совпадать с содержимым тех же ячеек , на 2-ом этаже будет копироваться содержимое левой полуленты: на нем в i-ой ячейке

будет тот же символ, что и в -i-ой ячейке

. Кроме того, на 3-ем этаже в 1-ой ячейке будет стоять отмечающий ее символ #. Таким образом, ?' = ? ? ? ? {, # } ?. Работа будет происходить следующим образом.

1) На первом этапе отмечается 1-я ячейка и содержимое входа переписывается на 1-ый этаж трехэтажной ленты:

Затем

моделирует работу , используя для работы на 2-ом этаже дубликаты состояний (со штрихами) и команды со сдвигами в обратном направлении. Для команды q ,a r , b ,C из P и для всех c ? в P' поместим команды:

Кроме того, для a =

сохраним и старые команды для работы на впервые посещаемых ячейках:

Сдвиги

из 1-ой ячейки налево в -1-ю и обратно моделируются переходом с одного этажа на другой в 1-ой ячейке

После завершения моделирования

результат записан в начальных ячейках на 1-ом этаже. переводит его в первоначальный алфавит ?.

Проверка правильности работы м.Т.

предоставляется читателю (см. задачу 9.4).

Основные определения

Рассматриваемая в этом разделе модель алгоритмов была предложена английским математиком Тьюрингом в 1937г. еще до создания современных компьютеров компьютеров1)

Он исходил из общей идеи моделирования работы вычислителя, оперирующего в соответствии с некоторым строгим предписанием. В машине Тьюринга расчленение процесса вычисления на элементарные шаги доведено в известном смысле до предела. Элементарным действием является замена одного символа в ячейке на другой и перемещение к соседней ячейке. При таком подходе процесс вычисления значительно удлиняется, но зато логическая структура процесса сильно упрощается и приобретает удобный для теоретического исследования вид.

Машина Тьюринга (м.Т.) состоит из неограниченной в обе стороны ленты, разбитой на ячейки, по которой передвигается головка машины. Такая "бесконечность" ленты является математической абстракцией, отражающей потенциальную неограниченность памяти вычислителя. Разумеется, в каждом завершающемся вычислении используется только конечная часть этой памяти - конечное число ячеек. В каждой ячейке ленты записан один символ из конечного внешнего алфавита машины ? = {a0, a1, … ,am }. Головка машины представляет конечный автомат, который в каждый момент времени находится в одном из внутренних состояний Q ={q0,q1,… , qn }. На каждом шаге головка в зависимости от своего внутреннего состояния и символа в ячейке, которую она наблюдает, изменяет свое внутреннее состояние и содержимое наблюдаемой ячейки и может сдвинуться на одну ячейку вправо или влево либо остаться на месте.

Дадим более формальное определение.

Определение 9.1. Машина Тьюринга - это система вида

включающая следующие компоненты:

Q ={q0,q1,… ,qn } - внутренний алфавит (алфавит состояний); ? = {a0, a1, … , a{m-1} } - внешний алфавит (алфавит ленты);

P - программа машины, в которой для каждой пары qi

Q \ { qf }, aj ? имеется (одна!) команда вида

C

{Л, П, Н} задает сдвиг головки вправо, влево или на месте;

q0

Q - начальное состояние;qf Q - заключительное состояние.

Выделим в алфавите ? специальный пустой символ a0 = и будем считать, что во всех ячейках ленты, кроме конечного их числа, в начальный и во все последующие моменты находится пустой символ.

Будем говорить, что некоторый символ стирается, если он заменяется на пустой. Два слова из ?* будем считать равными, если они совпадают после отбрасывания всех пустых символов слева и справа. Например, ab c = ab c = ab c, но ab c abc.

Как и для конечных автоматов, программу P можно задавать с помощью таблицы размера n ? m, строки которой соответствуют состояниям из Q, а столбцы - символам из входного алфавита ?, в которой на пересечении строки qi и столбца aj стоит тройка qk al C - правая часть команды qi aj qk al C.

Определение 9.2. Назовем конфигурацией м.Т. в некоторый момент времени слово K= wл qi aj wп, где wл ?* - слово на ленте левее текушего положения головки, qi - внутреннее состояние в данный момент, aj- символ, обозреваемый головкой, wп ?* - слово на ленте правее текушего положения головки.

Будем считать, что слово wл aj wп содержит все значащие символы на ленте. Поэтому, с точностью до описанного выше равенства слов, конфигурация определена однозначно. В частности, если wл=?, т.е. пусто, то левее положения головки все ячейки пусты, а если wп=?, то правее положения головки все ячейки пусты.

Начальная конфигурация - это конфигурация вида q0w, т.е. в начальный момент времени головка в состоянии q0 обозревает первый символ входного слова w. { it Заключительная } конфигурация - это конфигурация вида w1 qf w2, в которой машина находится в заключительном состоянии qf .

Определение 9.3. Скажем, что конфигурация K= w1 qi aj w2 м.Т. за один шаг (такт) переходит в конфигурацию если в программе имеется команда qi aj qk al C и при этом,

если С=Н, то w1'=w1, w2'=w2 и a{j'}=al;если С=Л, то w1=w1' a, a{j'}=a, w2'=al w2 (если w1=?, / то w1' = ? и a{j'}=);если С=П, то w2=aw2', a{j'}=a, w1'=w1 al (если w2=?, / то w2' = ? и a{j'}=).

Как обычно, через обозначим рефлексивное и транзитивное замыкание отношения а будет означать, что конфигурация K за n шагов переходит в K'. (Если из контекста ясно, о какой машине идет речь, то индекс будем опускать).

Последовательная и параллельная композиции машин Тьюринга

Используя возможность моделирования произвольной м.Т. на м.Т. со стандартными заключительными конфигурациями, легко установить справедливость следующей леммы о последовательной композиции машин Тьюринга.

Лемма 9.3.(Последовательная композиция) Пусть м.Т.

вычисляет функцию f(x), а м.Т. - функцию g(x). Тогда существует м.Т. вычисляющая функцию h(x) = f(g(x)).

Доказательство Действительно, пусть

а

Используя лемму 9.1, будем считать, что у

заключительные конфигурации стандартны. Тогда легко проверить, что функция h вычисляется следующей м.Т. где P= P1 P2 {qf2 a q01 aН | a ?2} .

Покажем, что работу двух м.Т. можно комбинировать так, чтобы в заключительной конфигурации содержались результаты работы каждой из них над независимыми входами.

Лемма 9.4. (Параллельная композиция) Пусть м.Т.

вычисляет функцию f(x), а м.Т. - функцию g(x) и символ * не входит в алфавит м.Т. . Тогда существует м.Т. которая по любому входу вида x*y выдает результат f(x)*g(y), т.е. вычисляет функцию H(x*y) = f(x)*g(y).

Доказательство. Пусть

и - м.Т. Не ограничивая общности, будем считать, что эти машины односторонние (по Лемме 2). Определим теперь м.Т. которая работает следующим образом.

Начав в конфигурации (p0x*y), находит 1-ый символ yи переходит в конфигурацию (x*q02y).Работая как

вычисляет g(y) и переходит при этом в конфигурацию (x*qf2g(y)).Переписывает *x после g(y) и переходит в конфигурацию g(y)*q01x).Работая как вычисляет f(x) и переходит при этом в конфигурацию (g(y)*qf1f(x).Меняет и местами и останавливается.

Корректность этапов 2 и 4 следует из односторонности

и а реализация этапов 1, 3 и 5 достаточно очевидна (см. задачу 9.6).

Построенную в этой лемме м.Т.

, полученную в результате параллельной композиции и , будем обозначать как . Здесь индекс * указывает символ, которым отделяются аргументы и

на ленте

. Этот символ может быть любым символом, не входящим в алфавит машины . Например, будет обозначать параллельную композицию машин и , в которой их аргументы отделены символом #.

Конструкцию параллельной композиции можно обобщить на произвольное конечное число машин Тьюринга.

Следствие. Пусть - машины Тьюринга, вычисляющие функции f1, … , fm, соответственно. Пусть символ * не входит в алфавиты этих машин. Тогда существует м.Т. , перерабатывающая любой вход вида x1*x2* … *xm (xi ?i*, i=1,…, m) в выход f1(x1)*f2(x2)* … *fm(xm).

Действительно, в качестве можно взять м.Т., определяемую выражением \\ Будем обозначать эту машину Тьюринга как .

Повторение (цикл)

Используя конструкцию для ветвления легко реализовать в терминах машин Тьюринга и оператор цикла.

Лемма 9.6. Пусть ? - распознающая м.Т., а м.Т.

вычисляет функцию f(x). Тогда существует м.Т. которая вычисляет функцию, задаваемую выражением:

Доказательство. Действительно, пусть м.Т.

- вычисляет тождественную функцию g(x)=x. Построим по м.Т.

м.Т.

реализующую ветвление как в лемме 9.5. Тогда искомая м.Т. получается из заменой команд qf1 a qf a H (a ?) на соответствующие команды qf1 a q0 a H (a ?), обеспечивающие зацикливание.

Реализованные выше операции над машинами Тьюринга и вычислимыми функциями позволяют получать программы новых м.Т., используя обычные конструкции языка программирования "высокого" уровня: последовательную и параллельную композицию, ветвление и цикл. Пусть M, M1, M2,… , Mm, ? - машины Тьюринга. Последовательную композицию M1 и M2 будем обозначать M1;M2, параллельную композицию M1, M2,… , Mm обозначаем как

(здесь b - это символ, разделяющий аргументы и результаты этих машин), ветвление -

цикл -

Пример 9.4. Рассмотрим в качестве примера задачу перевода чисел из унарной системы счисления в двоичную. Пусть fub(|n) = n(2) для всех n

N, где n(2) - двоичная запись числа n.

Пусть M1 - м.Т., которая начальную конфигурацию q0 ,|n переводит в конфигурацию q1 ,0*|n; M2 - м.Т., которая прибавляет 1 к двоичному числу-аргументу (см. пример ref{ex8-suc}); M3 - м.Т., которая вычитает 1 из унарного числа; ? - м.Т., которая на аргументе вида x*|y выдает 0, если число y > 0, и выдает 1 при y=0 (т.е. на аргументе x*

)); M4 - м.Т., которая стирает * в аргументе вида x* и останавливается. Реализация каждой из указанных м.Т. очевидна. Теперь требуемая м.Т. Mub, вычисляющая fub, получается как

Действительно, после работы M1 получаем конфигурацию q10*|n. Предположим теперь по индукции, что после i (i <n) итераций цикла while получается конфигурация q1 i(2)*|n-i. Тогда на (i+1)-ой итерации цикла после параллельного применения M2 к i(2) и M3 к |n-i

получаем конфигурацию q1(i+1)(2)*|n-i-1. Поэтому после n итераций получится конфигурация q1 n(2)*

. На ней ? выдаст 1, и цикл завершится с записью n(2)* на ленте, из которой M4 сотрет * и оставит требуемый результат n(2).

Отметим, что из приведенного примера и из задачи \oldref{prb3-6}(a) следует, что класс вычислимых на м.Т. арифметических функций не зависит от выбора унарного или двоичного кодирования аргументов и результатов. Это же справедливо и для троичной, десятичной и других позиционных систем счисления ( почему ?).

Стандартная заключительная конфигурация

Назовем заключительную конфигурацию стандартной, если в ней головка наблюдает первый значащий символ результата, который находится в 1-ой ячейке (т.е. в той же ячейке, где начиналось входное слово).

Лемма 9.1.Для всякой м.Т.

можно построить эквивалентную м.Т. у которой все заключительные конфигурации стандартны.

Доказательство. Пусть

Определим по ней м.Т. , которая удовлетворяет требованиям леммы. Положим ?' = ? { a' | a ?} { #}, где # - новый символ. работает следующим образом.

Отмечает символ в первой ячейке штрихом и переходит в начальное состояние

Далее работает как но сохраняет штрих в первой ячейке и вместо пустого символа записывает #. Для этого для каждой команды qiaj qk alC из P'в P' добавляется ее дубликат qiaj' qk al'C, в правых частях команд символ всюду заменяется на # и для каждой команды вида qi qk al C в P' добавляется команда qi # qk al C . После завершения этого этапа все посещенные в процессе работы головкой ячейки составляет непрерывный отрезок, не содержащий пустых символов.Далее стирает ненужные символы # слева и справа от блока ячеек, содержащего первую ячейку и все ячейки с символами результата, и переходит в одну из трех следующих конфигураций: где w - результат работы { cal M} (с заменой символов внутри w на #) и w1aw2 = w.Сдвигает в нужном направлении результат, совмещая его начало с ячейкой, помеченной штрихом, заменяет все # внутри w на , снимает штрих в 1-ой ячейке и останавливается. Например, для K1 это достигается с помощью следующих команд (мы предполагаем, что ни одно из используемых ниже состояний qл, q1, p, p1, p2, p3, pa, pa' (a ? { #}) не входит в Q): поиск левого конца w: qл a qлaП (a {#', #}); qлa q1a'П (a ?) (отметили первый символ w), qл p3 Л; (результат пуст); поиск правого конца w: q1 a q1aП (a ? { #} ), q1 p Л (в состоянии p наблюдает последний символ w); сдвиг результата на 1 ячейку влево: pa pa Л; pa b pb aЛ; pa b' pb'aП; pb' # p1 b'П; возврат к правому концу и переход к следующему сдвигу: p1 a p1aП (a ); p1 p Л; при сдвиге до 1-ой ячейки замена символов # на и удаление штриха:

Из построения непосредственно следует, что м.Т.

удовлетворяет требованиям леммы.

Тьюрингово программирование

В этом разделе мы приведем примеры вычислений на машинах Тьюринга и рассмотрим некоторые общие приемы, позволяющие комбинировать программы различных м. Т. для получения более сложных вычислений. Будем считать, что ячейки ленты м.Т. занумерованы от -? до +? , причем в начальной конфигурации головка находится в 1-ой ячейке:

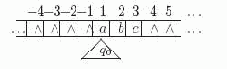
Рис. 9.2.  Нумерация ячеек ленты машины Тьюринга

Пример 9.2.Функция f(x)=x+1

Унарное кодирование.

Пусть м.Т.

где P1: q0 | q0 | П, q0 qf | Н.

Ясно, что м.Т.

проходит по массиву палочек слева направо и записывает в первой пустой ячейке новую |.

Бинарное кодирование.

Пусть м.Т.

где

Нетрудно видеть, что эта машина в состоянии q0 находит младший разряд двоичного входа, затем в состоянии q1, идя справа налево, заменяет единицы на нули до тех пор, пока не находит 0 (или

) и заменяет его на 1. Следовательно, м.Т. вычисляет функцию f(x) = x+1.

Пример 9.2. Копирование.

Рассмотрим функцию копирования (дублирования) слов в алфавите ?: copy(x)= x*x (мы предполагаем, что *

?).

Для ее реализации используем один из типичных приемов Тьюрингова программирования - { it расширение алфавита}.Пусть ?'= {a' | a

? } и ?1=? ?'. М.Т. копирующая вход, работает следующим образом:

отмечает 1-ый символ входа, идет направо, ставит * после входа и возвращается в начало:

в состоянии qa движется направо и записывает a в первую свободную ячейку: возвращается в отмеченную ячейку и передвигает метку ' на одну ячейку вправо, снова переходя в состояние q2: увидев символ * в состоянии q5, останавливается:

Из этого описания непосредственно следует, что

для любого x {?}*.

Ветвление (условный оператор)

Машину Тьюринга ? будем называть распознающей, если для некоторого алфавита ? и каждого входа x

?*, на котором ? останавливается, ее результат {?}(x) {0, 1}, т.е. ? вычисляет некоторую двузначную функцию (возможно частичную) на словах из ?.

Лемма 9.5. Пусть ? - распознающая м.Т., м.Т.

вычисляет функцию f(x), а м.Т. - функцию g(x). Тогда существует м.Т. вычисляющая функцию

Доказательство. Требуемая м.Т.

вначале копирует вход x и получает на ленте слово x*x, затем вычисляет параллельную композицию функций ?(x) и тождественной функции e(x)=x и переходит в конфигурацию p{?}(x)*x. Выбор между f и g происходит по следующим командам:

Кроме того, обеспечим переход в новое заключительное состояние:

Таким образом, мы реализовали в терминах машин Тьюринга обычный в языках программирования оператор ветвления:

для функции копирования, не увеличивая

Задача 9.1. Постройте м.Т. для функции копирования, не увеличивая исходный алфавит ?.
Задача 9.2. Постройте программу м.Т., которая выполняла бы перенос непустого слова в заданное место ленты, т.е. для любого слова w (? \ {})* и n > 0 выполняла преобразование конфигураций:
Задача 9.3. Достройте программу м.Т. из леммы 9.1 на этапах 3 и 4.
Задача 9.4. Докажите, что односторонняя м.Т. построенная в лемме 9.2, корректно моделирует исходную м.Т.
Задача 9.5. Другой, по сравнению с конструкцией леммы 9.2, подход к моделированию двухсторонней ленты на односторонней заключается в том, чтобы содержимое правой полуленты хранить в четных ячейках а содержимое левой полуленты - в нечетных, поместив в 1-ю ячейку специальный маркер. Постройте программу, реализующую этот подход (ее достоинство - увеличение алфавита ленты всего на 1 символ).
Задача 9.6. Достройте программу м.Т. из леммы 9.4 на этапах 1, 3 и 5.
Задача 9.7. Построить программы машин Тьюринга, вычисляющих следующие функции.
Перевод из двоичной системы в унарную: fbu(n(2))= |n.Сложение и вычитание в двоичной системе: sum(n*m)=n+m и совпадает с - при n m и при m > n).Умножение в двоичной системе: mul(n*m)= n ? m. ( Реализуйте алгоритм умножения "в столбик".)Возведение в степень: exp(n*m)= nm.Извлечение квадратного корня: .Логарифмирование: log(n)= log2n .Деление: Остаток от деления: rest(n*m) = n mod m.Функция выбора аргумента: .
Задача 9.8. Используя машины Тьюринга из предыдущей задачи, построить программы машин Тьюринга, вычисляющих следующие функции.









Задача 9.9. Докажите, что всякую арифметическую функцию f(x), вычислимую на некоторой м. Т. M = <Q, ?, P,q0, qf>, можно также вычислить на м. Т. M',, алфавит ленты которой содержит лишь два символа и |. (Указание: используйте для моделирования одного символа из ? блок из нескольких подряд идущих ячеек, содержащих его код в алфавите {, , | }) и замените каждую команду M группой команд, обрабатывающих соответствующий блок ячеек).


Задача 9.10.
Построить машину Тьюринга, определяющую по слову x в алфавите {1, 2} симметрично ли оно, т. е. вычисляющую функцию:

Задача 9.11.
Построить машину Тьюринга, сравнивающую два слова x=x1x2… xn и y=y1y2… ym в алфавите {1, 2, 3} лексикографически: или для некоторого непустого слова x' выполнено y = x x'. Эта машина Тьюринга должна вычислять функцию:

---

---