Ортогональность собственных форм колебаний

При колебаниях системы по первой собственной форме наибольшие отклонения равны

; этим отклонениям соответствуют силы инерции

. Аналогично при колебаниях по второй собственной форме наибольшие отклонения составляют

и соответствующие силы инерции равны

Применим к этим двум состояниям теорему Бетти о взаимности виртуальных работ. Согласно этой теореме, работа сил первого состояния

на перемещениях второго состояния

равна работе сил второго состояния

на перемещениях первого состояния

, т.е.

или

Так как

, то должно выполняться равенство:

Это равенство выражает свойство ортогональности двух собственных форм колебаний. После деления на

условие ортогональности можно также записать в виде

Если известно отношение

, определяющее первую собственную форму, то из условия ортогональности можно найти отношение

, соответствующее второй собственной форме:

Обобщая всё сказанное выше, можно отметить, что для любой системы с n степенями свободы выполняется условие ортогональности любых двух собственных форм.

Основное уравнение

Из курса сопротивления материалов известны дифференциальные зависимости при изгибе балок:

; (189)

, (190)

где EJ - жёсткость при изгибе; y=y(x, t) - прогиб; M=M(x , t) - изгибающий момент; q - интенсивность распределённой нагрузки.

Объединяя (189) и (190), получим

. (191)

В задаче о свободных колебаниях нагрузкой для упругого скелета являются распределённые силы инерции:

где m - интенсивность массы балки (масса единицы длины), и уравнение (191) принимает вид

В частном случае постоянного поперечного сечения, когда EJ = const, m = const, имеем:

. (192)

Для решения уравнения (192) полагаем, как и выше,

y = X (x)× T (t). (193)

Подставляя (193) в (192), приходим к уравнению:

Для тождественного выполнения этого равенства необходимо, чтобы каждая из частей равенства была постоянной. Обозначая эту постоянную через

, получим два уравнения:

; (194)

. (195)

Первое уравнение указывает на то, что движение носит колебательный характер с частотой

Второе уравнение определяет форму колебаний. Решение уравнения (195) содержит четыре постоянных и имеет вид

где

. (196)

Удобно использовать вариант записи общего решения, предложенный А.Н.Крыловым:

, (197)

где

(198)

представляют собой функции А.Н.Крылова.

Обратим внимание на то, что S=1, T=U=V=0 при x=0. Функции S,T,U,V связаны между собой следующим образом:

(199)

Поэтому производные выражения (197) записываются в виде

(200)

В задачах рассматриваемого класса число собственных частот

бесконечно велико; каждой из них отвечает своя функция времени Tn и своя фундаментальная функция Xn. Общее решение получится путём наложения частных решений вида (193)

. (201)

Для определения собственных частот и формул необходимо рассмотреть граничные условия.

Основное уравнение (уравнение Матье)

В ряде случаев параметры механической системы - ее жесткость или масса - не остаются неизменными, а являются некоторыми заданными функциями времени, чаще периодическими. Если нарушить состояние равновесия такой системы, то будут происходить своеобразные колебания: с одной стороны, их нельзя назвать свободными, так как система испытывает определенное внешнее воздействие в виде изменения жесткости, а с другой - они не являются вынужденными, так как внешнее воздействие не проявляется в виде заданной возмущающей силы. Эти колебания называются параметрическими и в зависимости от свойств системы и характера изменения ее параметров могут иметь ограниченные или возрастающие амплитуды, причем во втором случае возможно наступление параметрического резонанса.

Рассмотрим простейшую систему (рис.56). Сосредоточенная масса 1 закреплена на конце невесомого стержня 2. Свобода перемещений стержня дополнительно ограничена втулкой 3, удаленной от нижнего конца стержня на расстояние

Рис. 56

Составим уравнение свободных колебаний груза, считая, что они происходят в плоскости чертежа. Если в текущий момент времени t перемещение груза составляет x, то восстанавливающая сила упругости стержня равна -cx, а уравнение движения груза имеет вид

где c - коэффициент жесткости системы.

Втулка 3 при ее достаточной длине обеспечивает практически полное защемление нижней части стержня, и тогда

. При этом предполагается, что стержень имеет постоянное поперечное сечение с осевым моментом инерции

. Таким образом, дифференциальное уравнение движения

(148)

Если расстояние

постоянно, то (148) описывает свободные колебания массы

около ее среднего положения с собственной частотой

Теперь предположим, что втулка 3 скользит вдоль стержня 2 по заданному закону

т.е. совершает около среднего положения

гармонические колебания с амплитудой А и круговой частотой

. В этом случае коэффициент жесткости оказывается функцией времени:

(149)

и дифференциальное уравнение (148) становится уравнением с переменными

коэффициентами:

(150)

что характерно для системы с параметрическим возбуждением колебаний.

Существует много других механических систем, подверженных параметрическому возбуждению. Ряд примеров убеждает, что в большинстве практически важных случаев дифференциальное уравнение параметрических колебаний можно привести к стандартной форме:

(151)

где a и q - некоторые постоянные.

Возвращаясь к механической системе, показанной на рис.56, положим, что амплитуда колебаний втулки A весьма мала по сравнению с длиной

, тогда вместо (149) приближенно получается

(152)

и дифференциальное уравнение (150) принимает вид

(153)

Перейдем к безразмерному времени

тогда

и дифференциальное уравнение (153) приобретает стандартную форму (151),

причем

(154)

Основное уравнение параметрических колебаний (151) называется уравнением Матье. Решения этого уравнения носят колебательный характер и главным образом зависят от конкретных значений параметров a и q. В одних случаях данной комбинации a и q соответствуют колебания, ограниченные по амплитуде, а в других - колебания с возрастающими амплитудами. Основную практическую важность представляет именно тенденция колебательного процесса: если амплитуды остаются ограниченными, то система устойчива; в противном случае имеет место параметрический резонанс, и система неустойчива.

Результаты решения уравнения Матье для двух различных комбинаций a и q показаны на рис.57 (эти решения получены при помощи электронного аналогового устройства). Хотя в обоих случаях параметр q системы одинаков (q = 0,1), колебания имеют совершенно разный характер из-за различия между значениями параметра a (a = 1; a = 1,2). В первом случае амплитуды возрастают, т.е. система неустойчива, а во втором случае остаются ограниченными, т.е. система устойчива.

Для практических целей наибольшее значение имеют границы между областями устойчивых и неустойчивых решений. Этот вопрос хорошо исследован, причем окончательные результаты представляются в виде диаграммы, построенной в плоскости параметров a и q, которая называется диаграммой Айнса-Стретта.

Каждой данной системе, характеризуемой параметрами a и q, соответствует точка с координатами a, q на диаграмме Айнса-Стретта (изображающая точка). Если изображающая точка находится в пределах заштрихованных полей диаграммы, то система устойчива; неустойчивым системам соответствуют изображающие точки, расположенные на белых полях.

Рис. 57

На рис.58 показана часть диаграммы Айнса-Стретта, относящаяся к малым значениям параметра q. В качестве примера на диаграмме указаны точки 1 и 2, соответствующие параметрам a1 = 1; q1 = 0,1; a2 = 1,2; q2 = 0,1 (решения уравнения Матье для этих случаев даны на рис.57).

Рис. 58

Точка 1 находится в белой зоне (неустойчивость), и колебания происходят с возрастающими амплитудами (рис.57,а). Точка 2 находится в пределах заштрихованной зоны; ей отвечает движение с ограниченной амплитудой (рис.57,б).

В плоскости параметров a, q области устойчивости чередуются с областями неустойчивости, причем наиболее широкая, а потому и наиболее важная область неустойчивости содержит точку a = 1, q = 0. Диаграмма Айнса-Стретта полностью освобождает от выполнения каких-либо операций по решению уравнения Матье. Достаточно составить это уравнение, т.е. найти значения параметров системы a и q, после чего диаграмма дает ответ на вопрос об устойчивости или неустойчивости системы.

При возрастании частоты возбуждения параметры a и q уменьшаются. Так как отношение этих параметров остается постоянным, то последовательные состояния системы определяются изображающими точками на луче

, проходящем через начало координат.

Пластина, шарнирно опертая по противолежащим сторонам

Точное решение задачи об определении собственных частот и форм колебаний прямоугольной пластины может быть получено, если две противолежащие стороны пластины имеют шарнирное опирание. При этом закрепление двух других сторон может быть произвольным.

Пусть у прямоугольной пластины размерами (

- размер вдоль оси

;

- вдоль оси

) шарнирно оперты края

Тогда выражение для амплитудных прогибов, удовлетворяющее условиям шарнирного опирания на этих краях, можно представить в виде

Подставляя это выражение в (318) и (319), устанавливаем, что функция

должна удовлетворять одному из двух уравнений:

где

или

где

Решениями этих уравнений являются выражения

Следовательно, общее выражение для

принимает вид

Это выражение должно удовлетворять граничным условиям при

Если эти края пластины также шарнирно оперты, то должно быть

Из условий при

находим

Условия при

приводят к уравнениям

Приравнивая нулю определитель этой системы уравнений, получим частотное уравнение

которое выполняется при

Так как

, то

Тогда собственные частоты пластинки, шарнирно опертой по контуру, определяются формулой

(320)

где

Низшая частота

соответствует

т.е. колебаниям пластинки без узловых линий:

Форма колебаний определяется выражением

(321)

Аналогичным образом проводится расчет и при других условиях закрепления границ

Позиционное трение

Так называется вид трения, при котором сила трения пропорциональна смещению. Рассмотрим систему, состоящую из груза массой m, закреплённого на рессоре, листы которой собраны без предварительного натяга (рис. 20,а). Сила трения листов рессоры друг от друга пропорциональна контактному давлению, которое, в свою очередь, пропорционально смещению

. Зависимость между реакцией рессоры, действующей на груз, и смещением груза

F=¦

для рассматриваемой системы представлена на рис. 20,б.

Обозначим жёсткость системы при увеличении смещения

по модулю через С

, а жёсткость при уменьшении абсолютного значения смещения - через С

. Жёсткость упругого элемента системы при отсутствии трения

а б

Рис. 20

На каждой четверти периода характеристика системы прямолинейна, поэтому движение массы m описывается синусоидой. При переходе через равновесное положение частота собственных колебаний меняется от

до

. Отклоним массу m в крайнее правое положение, при этом её скорость в этот момент

. Если груз отпустить, то он начнёт двигаться влево под действием силы упругости, уменьшенной на величину сил трения. Частота собственных колебаний груза будет

, а время движения до равновесного положения -

. Скорость груза в равновесном положении станет равной

. Дальнейшее движение (влево) определяется жёсткостью

, а крайнего левого положения груз достигает через время

. Наибольшее смещение влево равно

Максимальное отклонение вправо в конце полного периода движения вычисляется по формуле

следовательно, логарифмический декремент колебаний:

При малом затухании, когда разность жесткостей

существенно меньше средней жёсткости

, получим

Характер движения при позиционном трении показан на рис. 21. Из полученных формул следует, что при силе трения, пропорциональной смещению, логарифмический декремент колебаний постоянен и, следовательно, точно так же, как и при вязком трении, последовательные амплитуды составляют геометрическую прогрессию.

Рис. 21

Как видно из рис. 21, период рассматриваемых затухающих колебаний:

.

Соответствующая этому периоду угловая частота:

.

Частоты

определяются выражениями

;

,

где

- собственная частота соответствующей системы без трения.

Тогда

.

При небольших логарифмических декрементах колебаний

это выражение отличается от собственной частоты колебаний соответствующей системы без трения на величину второго порядка малости. Поэтому подобно вязкому и сухому трению позиционное трение практически не влияет на собственную частоту колебаний.

Приближённые методы расчета колебаний

Рассмотренные выше методы расчета становятся тем более громоздкими, чем сложнее структура рассчитываемой системы. Поэтому возникает необходимость в способах, позволяющих достаточно просто рассчитывать и сложные системы.

Один из возможных путей состоит в применении простых приближенных формул (например, формулы Рэлея). В этом случае задают форму колебаний системы, сводя её таким образом к системе с одной степенью свободы. При удачной аппроксимации получают достаточно точное значение низшей собственной частоты системы, однако другие её динамические характеристики остаются нераскрытыми.

Cхематизация реальной системы, как имеющей несколько степеней свободы, достигается в методе Рэлея-Ритца, при использовании которого форма колебаний системы задаётся в виде выражения, включающего несколько параметров.

Другим приёмом, позволяющим свести реальную систему к системе с конечным числом степеней свободы, является метод прямой дискредитации. Чем больше число элементов, на которые разбита система при использовании этого метода, тем ближе расчётная схема к исходной системе. Вместе с тем, если элементы выбраны однотипными, то даже при большом их числе оказывается возможным реализовать расчёт колебаний, используя матричные методы с применением ЭВМ. Примерами таких методов являются метод начальных параметров в форме матриц перехода и метод прогонки.

При динамических расчётах конструкций сложной конфигурации также широко используется метод конечных элементов.

В том случае, когда сложную колебательную систему можно разделить на несколько подсистем, динамические характеристики которых определяются сравнительно просто, полезными являются методы динамических податливостей и жёсткостей. Эти методы представляют собой обобщение на динамические задачи метода сил и метода перемещений строительной механики.

В методе последовательных приближений задача об определении собственных частот и форм колебаний сводится к многократному расчёту деформаций системы под действием известной статической нагрузки.

Рассмотрим некоторые из используемых приближённых методов.

Применение метода Рэлея-Ритца к определению частот собственных колебаний пластинок

Метод Рэлея-Ритца позволяет расчетным путем приближенно определять частоты собственных колебаний пластинок переменной толщины и, в частности, дисков турбомашин. Преимуществом этого метода является также возможность легко учесть влияние на частоту различных побочных факторов, например начальных напряжений в срединной поверхности пластинки.

Потенциальная энергия деформации пластинки при ее изгибе по форме, определяемой функцией

, выражается двойным интегралом

(333)

где

; интеграл берется по всей поверхности пластинки, причем для пластинки постоянной толщины, заделанной по контуру, интеграл от второго слагаемого выражения (333) обращается в нуль.

Обобщенная масса пластинки

(334)

В соответствии с методом Рэлея-Ритца форма колебаний задается в виде ряда

(335)

где каждая из координатных функций

удовлетворяет геометрическим граничным условиям.

Равенство нулю определителя системы уравнений

(336)

позволяет определить частоты собственных колебаний.

Если в (335) ограничиваются одним слагаемым, то частота определяется по формуле Рэлея

(337)

Можно задаваться выражением для формы колебаний, в которое параметры

входят нелинейно

В этом случае уравнения метода Рэлея-Ритца (336) оказываются нелинейными и проще исходить не из них, а из условий экстремума выражения (337), причем значения параметров, при которых достигается этот экстремум, находятся численными методами.

Рассмотрим в качестве примера заделанную по контуру прямоугольную пластинку постоянной толщины. Ограничиваясь одним слагаемым выражения (335), принимаем

Проводя вычисления по (333) и (334), находим

Для частоты колебаний получаем

При

что на 3,3 % выше точного значения.

При расчете колебаний круглых пластин целесообразно использовать выражения энергии деформации и обобщенной массы в полярных координатах

где интегрирование выполняется по всей срединной поверхности пластинки.

При изучении колебаний осесимметричных пластин полагают

В этом случае интегрирование по

можно выполнить в общем виде и выражения для

представляются в форме

(338)

(339)

Для сплошной свободной пластинки вычисления упрощаются, если принять функцию

в виде

где

- параметр, определяемый из условия минимума формулы Рэлея (337).

Тогда

определяются формулами

Чтобы оценить погрешность метода, применим его для расчета частоты колебаний диска постоянной толщины при двух узловых диаметрах. В этом случае

;

Отсюда находим

Минимальное значение частоты при

что дает ошибку порядка 5 %.

Пример 17. Два двигателя массой

Пример 17. Два двигателя массой m = 500 кг каждый установлены на двух балках двутаврового сечения №24 (рис.53,а). При работе левый двигатель создает возмущающую силу

. Найти амплитуды колебаний двигателей и максимальное напряжение в балках без учета массы балок. Дано: a = 2 м; F = 1кн; n = 480 об/мин;

кПа.

К цилиндрической пружине подвешен груз

Пример 1. К цилиндрической пружине подвешен груз массой
m = 2 кг = 2

. Груз может перемещаться только в вертикальном направлении. Определить частоту собственных колебаний груза без учёта и с учётом массы пружины. Средний диаметр пружины D = 6 см; диаметр проволоки пружины d = 0,6 см; число витков n = 15; плотность материала

; модуль сдвига G =

.
Решение.
Жесткость пружины:

.
Частота собственных колебаний без учёта массы пружины :

.
Приведенная масса пружины:

Частота собственных колебаний с учётом массы пружины:

.
Пример 2. Определить круговую и техническую частоту, а также период собственных колебаний сосредоточенного груза Р = 12 кН, приложенного на свободном конце балки, жестко заделанной другим концом. Балка представляет собой двутавр № 20 (Jx = 1840 см4) длиной

= 1 м. Собственным весом балки пренебречь.
Решение.
Статический прогиб балки от веса сосредоточенного груза:

.
Частота собственных колебаний:

.
Период колебаний:

.
Техническая частота:

.
Пример 3. К стальному стержню подвешен груз массой m = 50 кг, совершающий вертикальные продольные колебания. Длина стержня

= 1 м, диаметр d = 2 см. Определить частоту и период собственных вертикальных колебаний системы без учёта и с учётом массы стержня.
Решение.
Жесткость стержня:

.
Частота собственных колебаний без учёта массы стержня:

.
Соответствующий период колебаний:

.
Приведенная масса стержня:

.
Собственная частота колебаний с учётом массы стержня:

.
Соответствующий период колебаний:

.
Пример 4.
Определить собственную частоту крутильных колебаний двухмассовой системы (рис. 14,а) при следующих данных: диаметры дисков d1 =0,30 м; d2 = 0,20 м; толщины дисков b1 = 0,02 м; b2 = 0,015 м; диаметр вала d0 = 0,01 м; длина вала

= 0,8 м.

Рис. 14
Решение.
Дифференциальное уравнение свободных колебаний такой системы имеет вид

,
где

- взаимный угол поворота дисков,

- собственная частота колебаний.
Моменты инерции масс дисков:

;

.
Полярный момент инерции поперечного сечения вала:

.
Коэффициент жесткости вала при кручении:

.
Собственная частота крутильных колебаний:

.

Пример 6. Пружина несёт две массы

каждая - одна на конце пружины, другая посередине (рис. 28,а). Средний диаметр пружины

; диаметр проволоки пружины

; число витков на каждой половине пружины

. Определить частоты собственных колебаний системы.
а б

Рис. 28
Решение
Уравнения движения системы

где

- смещения верхней и нижней масс соответственно; С - жёсткость пружины.
Решение системы уравнений ищем в виде

После подстановки получим систему однородных алгебраических уравнений

Частотное уравнение

,
или

.
Корни частотного уравнения:

;

.
Жёсткость пружины:

.
Собственные частоты:

.
Пример 7. Определить частоты собственных колебаний невесомой консольной балки с двумя равными сосредоточенными массами (рис. 29,а). Построить собственные формы колебаний, проверить их ортогональность.

Пример №12. Ротор электродвигателя, установленного на консоли (рис.46,а), имеет частоту вращения n=900

Вследствие неуравновешенности ротора возникает вертикальная переменная сила

.Определить: 1) при каком значении

наступает резонанс; 2) на каком расстоянии

нужно установить двигатель, чтобы частота собственных колебаний балки была на 30 % больше частоты возмущающей силы. Для этого случая вычислить амплитуду вынужденных колебаний и максимальное нормальное напряжение. Массой балки пренебречь. Масса двигателя m=100 кг; амплитуда возмущающей силы

Продольные колебания стержней

При анализе продольных колебаний прямолинейного стержня (рис.67,а) будем считать, что поперечные сечения остаются плоскими и что частицы стержня не совершают поперечных движений, а перемещаются только в продольном направлении.

Рис. 67

Пусть u - продольное перемещение текущего сечения стержня при колебаниях; это перемещение зависит от расположения сечения (координаты x) и от времени t. Таким образом,

есть функция двух переменных; её определение и представляет основную задачу. Перемещение бесконечно близкого сечения равно

, следовательно, абсолютное удлинение бесконечно малого элемента

равно

(рис.67,б), а относительное его удлинение

Соответственно продольная сила в сечении с координатой х может быть записана в виде

, (173)

где

жёсткость стержня при растяжении (сжатии). Сила N также является функцией двух аргументов – координаты х и времени t.

Рассмотрим элемент стержня, расположенный между двумя бесконечно близкими сечениями (рис.67,в). К левой грани элемента приложена сила N, а к правой – сила

. Если обозначить через

плотность материала стержня, то масса рассматриваемого элемента составляет

. Поэтому уравнение движения в проекции на ось х

или

. (174)

Учитывая (173) и принимая A = const , получим

, (175)

где

. (176)

Следуя методу Фурье, ищем частное решение дифференциального уравнения (175) в виде

, (177)

т.е. предположим, что перемещение u можно представить в виде произведения двух функций, одна из которых зависит только от аргумента х, а другая только от аргумента t. Тогда вместо определения функции двух переменных u (x, t) необходимо определять две функции X(x) и T(t), каждая из которых зависит только от одной переменной.

Подставив (177) в (174), получим

где штрихами обозначена операция дифференцирования по x, а точками – по t.
Перепишем это уравнение таким образом:

.

Здесь левая часть зависит только от x,а правая – только от t. Для тождественного выполнения этого равенства (при любых x и t) необходимо, чтобы каждая из его частей была равна постоянной, которую обозначим через

;

. (178)

Отсюда следуют два уравнения:

;

. (179)

Первое уравнение имеет решение:

, (180)

указывающее на колебательный характер, причём из (180) видно, что неизвестная величина

имеет смысл частоты свободных колебаний.

Второе из уравнений (179) имеет решение:

, (181)

определяющее форму колебаний.

Частотное уравнение, определяющее величину

, составляется путём использования граничных условий. Это уравнение всегда трансцендентное и имеет бесконечное число корней. Таким образом, число собственных частот бесконечно, причём каждому значению частоты

соответствует своя функция Tn(t), определяемая зависимостью (180), и своя функция Xn(x), определяемая зависимостью (181). Решение (177) является лишь частным и не даёт полного описания движения. Полное решение получается путём наложения всех частных решений:

.

Функции Xn(x) называются собственными функциями задачи и описывают собственные формы колебаний. Они не зависят от начальных условий и удовлетворяют условию ортогональности, которое при А=const имеет вид

, если

.

Рассмотрим некоторые варианты граничных условий.

Закреплённый конец стержня (рис.68,а). В концевом сечении перемещение u должно быть равно нулю; отсюда следует, что в этом сечении

X=0 (182)

Свободный конец стержня (рис.68,б). В концевом сечении продольная сила

(183)

должна тождественно равняться нулю, что возможно, если в концевом сечении X'=0.

Упругозакреплённый конец стержня (рис.68,в).

При перемещении u концевого стержня возникает упругая реакция опоры

, где Со - жёсткость опоры.

Учитывая (183) для продольной силы, получим граничное условие

,

если опора расположена на левом конце стержня (рис.68,в), и

,

если опора расположена на правом конце стержня (рис.68,г).

Рис. 68

Сосредоточенная масса

на конце стержня.

Развиваемая массой сила инерции:

.

Так как, согласно первому из уравнений (179),

, то сила инерции может быть записана в виде

. Получаем граничное условие

,

если масса находится на левом конце (рис.68,д), и

, (184)

если масса связана с правым концом (рис.68,е).

Определим собственные частоты консольного стержня (рис.68,a').

Согласно (182) и (183), граничные условия

X=0 при х=0;

X'=0 при х=

.

Подставляя поочерёдно эти условия в решение (181), получим

D=0;

.

Условие С

0 приводит к частотному уравнению:

.

Корни этого уравнения

(n=1,2,…)

определяют собственные частоты:

(n=1,2,…). (185)

Первая (низшая) частота при n=1:

.

Вторая частота (при n=2):

и т. д.

Определим собственные частоты стержня с массой

на конце (рис.68,е).

Согласно (182) и (184), имеем

X=0 при х=0;

при х=

.

Подставляя эти условия в решение (181), получим:

D=0;

.

Следовательно, частотное уравнение при учёте (176) имеет вид

.

Здесь правая часть представляет собой отношение массы стержня к массе концевого груза.

Для решения полученного трансцендентного уравнения необходимо воспользоваться каким-либо приближённым способом.

При

значения наиболее важного низшего корня

будут соответственно 0.32 и 0.65 .

При малом отношении

решающее влияние оказывает груз и хорошие результаты даёт приближённое решение

.

Для стержней переменного сечения, т.е. при А

const, из (173) и (174) получается уравнение движения в виде

.

Это дифференциальное уравнение не поддаётся решению в замкнутом виде. Поэтому в подобных случаях приходится прибегать к приближённым методам определения собственных частот.

Разложение решения по собственным формам колебаний

Вновь рассмотрим простейшую систему, испытывающую действие возмущающих сил

Для вывода основных зависимостей рассматриваемого способа предварительно образуем вспомогательные соотношения исходя из уравнений (32). Эти уравнения удовлетворяются как решениями

(126)

так и решениями

(127)

Подставляя в уравнения (32) сначала решения (126), а затем решения (127), получим две группы вспомогательных соотношений, которые будут использованы в дальнейшем

(128)

(129)

В дифференциальных уравнениях (122) неизвестными являются функции

. Основная идея рассматриваемого способа состоит в замене этих функций двумя новыми функциями

такими, что

(130)

где

произвольные пока числа (можно, например, принять

), с которыми

связаны известными соотношениями (собственные формы колебаний). Подставляя (130) в (122), получим систему дифференциальных уравнений относительно новых функций

(131)

Уравнения (131) можно существенно упростить. При помощи полученных выше вспомогательных соотношений (128) и (129) перепишем (131) в виде

(132)

Дальнейшие упрощения вытекают из свойств ортогональности собственных форм колебаний. Умножим первое из уравнений (132) на

, а второе - на

и сложим их:

Согласно свойству ортогональности,

и из записанного уравнения выпадают функция

и её вторая производная

; в результате получается дифференциальное уравнение, содержащее только функцию

(133)

Аналогично можно получить дифференциальное уравнение, содержащее только функцию

. Для этого нужно первое из уравнений (132) умножить на

, второе - на

и полученные уравнения сложить. Используя затем то же свойство ортогональности, будем иметь

(134)

Таким образом, способ разложения по собственным формам колебаний приводит к раздельным уравнениям (133) и (134), каждое из которых описывает колебания некоторой системы с одной степенью свободы.

Этот способ требует предварительного расчёта частот и форм собственных колебаний, после чего расчёт на вынужденные колебания становится сравнительно простым.

Будем считать, что известны как собственные частоты

(число собственных частот равно

, а не

, так как одна частота равна нулю и соответствует повороту вала и дисков как жёсткого целого), так и соответствующие формы колебаний (т.е. отношения между амплитудами

первой собственной формы;

второй собственной формы и т.д.).

Системе уравнений (65), описывающих свободные колебания рассматриваемой системы, удовлетворяют функции, определяющие любое

главное колебание:

(143)

Подставляя (143) в систему уравнений (65), получим вспомогательные соотношения:

(144)

Произведём замену переменных в системе уравнений (139), введя новые функции

, которые связаны с функциями

следующим образом:

(145)

Функция

, общая для всех уравнений системы (145), соответствует вращению системы как жёсткого целого, т.е. нулевой собственной форме колебаний. Коэффициенты первой строки

принимаются любыми (например,

), тогда значения остальных коэффициентов определяются соответствующими собственными формами.

Подставляя (145) в систему уравнений (139), получим

Если учесть вспомогательные соотношения (144), то запись уравнений упрощается:

или после преобразований

(146)

Эта система уравнений распадается на независимые уравнения, если, как и выше, воспользоваться свойством ортогональности. Сложим все уравнения (146). Тогда первые слагаемые правых частей дадут сумму:

а вторые слагаемые -

Эта сумма вторых слагаемых равна нулю, так как сумма в первой скобке обращается в нуль вследствие ортогональности первой и нулевой форм колебаний. Точно так же обращаются в нуль результаты суммирования всех следующих слагаемых, входящих в правые части уравнений (146). Поэтому после сложения всех уравнений (146) получим

Интегрируя это уравнение, можно найти функцию f0.

Если обозначить правые части дифференциальных уравнений (133) и (134) соответственно через

, где

то стационарная часть решения имеет вид

Подставляя

в соотношения (130), получим решения для обобщённых координат

Приведенные выше действия обеспечивают разделение уравнений при любом конечном числе степеней свободы системы.

Разложение решения по собственным формам колебаний при сохранении заданного вида периодических нагрузок

Основное преимущество рассмотренного выше способа - разделение уравнений - никак не связано с тем или иным конкретным видом возмущающих сил. Иначе говоря, разделение уравнений так же легко достигается в случае произвольно заданных возмущающих сил

, как и в рассмотренном случае гармонических возмущающих сил

. Не повторяя выкладок, сразу приведём окончательные дифференциальные уравнения для общего случая

Такие уравнения легко интегрируются при любом виде правых частей. Таким образом, способ разложения решения по собственным формам колебаний не требует предварительного разложения возмущающих сил на гармонические составляющие. Такое разложение является достаточно громоздкой операцией и, как правило, требует учёта большого числа гармоник. Эта операция оправдана только при решении задачи первым способом.

Затем, умножив первое из уравнений (146) на А11, второе - на А21, третье - на А31 и т.д., сложим все полученные уравнения. При этом первые слагаемые правых частей образуют произведение:

причем сумма, заключенная в скобки, равна нулю. Суммирование вторых слагаемых дает отличное от нуля выражение

При суммировании третьих слагаемых получим

Вследствие ортогональности первых двух форм колебаний сумма в первой скобке, а следовательно, и все это выражение равно нулю. Аналогично равна нулю сумма четвертых слагаемых, пятых и т.д.

Окончательно получим дифференциальное уравнение, содержащее только одну функцию f1

Аналогично можно получить дифференциальное уравнение для функции f2. Для этого нужно умножить первое из уравнений (146) на А12, второе - на А22, третье - на А32 и т.д. Последовательно применяя тот же прием, можно образовать отдельные уравнения для остальных неизвестных функций. Для i-й функции fi дифференциальное уравнение имеет вид

(147)

Уравнения этого типа наиболее удобны, так как с их помощью задача о колебаниях системы с n степенями свободы заменяется n простыми задачами о колебаниях системы с одной степенью свободы. При практическом расчете крутильных колебаний валов существенными оказываются решения, соответствующие первым двум-трем собственным формам колебаний, а это означает, что достаточно решения двух-трех уравнений типа (147), когда i = 1,2,3.

При периодичности внешних возмущающих моментов правые части дифференциальных уравнений также будут периодическими функциями. Для дальнейшего решения обычно производят разложение каждого из возмущающих моментов в ряд Фурье, после этого анализируется влияние каждой гармоники, а затем выполняется сложение всех найденных результатов.

Хотя все эти выкладки выполняются достаточно просто, они должны быть повторены для всех важнейших гармонических составляющих возмущения, а число таких гармоник достаточно велико. Следующий пример (табл. 6) дает представление об относительной важности различных гармоник возмущения в частном случае одного четырехтактного двигателя внутреннего сгорания.

Как видно, амплитуды гармоник убывают очень медленно, и в данном случае необходимо учесть в расчете не менее 13-15 гармоник. Еще раз подчеркнем, что разложение возмущающих моментов в ряд Фурье необязательно, если решение находится при помощи уравнения (147).

Таблица 6

Номер составляющей	1	2	3	4	5	6	7	8	9	10
Амплитуда составляющей	2,38	2,69	2,65	2,31	1,95	1,64	1,01	0,76	0,59	0,47

Ввиду того, что угловая скорость вращения может изменяться в процессе эксплуатации, частоты возмущения

непостоянны; вместе с изменением режима вращения изменяются и частоты возмущения. При этом становится реальной возможность совпадения частоты какой-либо гармоники возмущения с одной из собственных частот. В случае такого совпадения система оказывается в резонансном режиме и в расчет амплитуд колебаний следует ввести силы неупругого сопротивления.

Полное решение такой задачи даже в простейшем предположении вязких сил трения оказывается очень громоздким, поэтому практические расчеты производят приближенными способами. Основное упрощение состоит обычно в том, что форма колебаний при резонансе принимается совпадающей с соответствующей собственной формой, определенной без учета сил затухания.

Пусть, например, одна из гармоник возмущающей силы имеет частоту

, равную i-й собственной частоте

. Тогда в расчете колебаний учитывается только i-я собственная форма, и если имеет место вязкое трение, то вместо уравнения (147) получим

где

- коэффициент затухания, зависящий от номера резонирующей гармоники;

- приведенная амплитуда возмущающей силы.

Это уравнение по смыслу совпадает с уравнением (106). Согласно (110), резонансная амплитуда в данном случае,

После вычисления резонансного значения

следует образовать резонансные значения амплитуд углов поворота. При помощи формул (145) получим, опуская в каждой строке как малые все слагаемые, кроме i-го:

в точках расположения масс m1

Прикладываем поочередно силу

в точках расположения масс m1 и m2 и строим эпюры изгибающих моментов

(рис. 29,б).

Путем перемножения соответствующих эпюр способом Верещагина вычисляем единичные перемещения:

Частотный определитель:

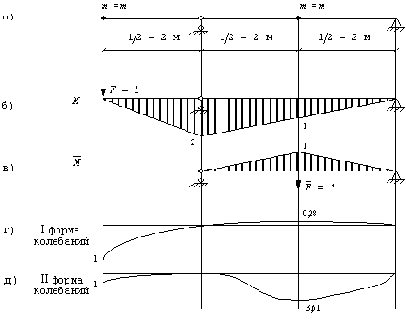
Рис. 29
или

где

Частотное уравнение:

Собственные частоты колебаний:

Система алгебраических уравнений относительно амплитуд колебаний А1 и А2:

Полагая А1=1, находим А2 из первого уравнения системы сначала при

, а затем при

Формы колебаний представлены на рис. 29,г,д.
Проверяем выполнение условия ортогональности:

Пример 8. Определитель частоты свободных колебаний балки с тремя равными сосредоточенными массами m (рис. 30,а), если m=0,5

;

=8 м;

Решение
Так как система и расположенные на ней массы симметричны, то задача может быть решена с использованием симметрии.
Строим единичные эпюры изгибающих моментов

(рис. 30,б,в,г).
Вычисляем единичные перемещения путем перемножения соответствующих эпюр по способу Верещагина:
.

Рис. 30

Определитель для симметричных колебаний составляем с учетом того, что перемещения от групповой силы

, состоящей из двух сил, получились удвоенными, поэтому соответствующая масса вводится с коэффициентом 0,5:

,
или

Соответствующее частотное уравнение:

Собственные частоты симметричных колебаний:

Частотное уравнение для обратно симметричных колебаний:

Пример 9. Определить собственные частоты и формы колебаний системы, состоящей из трех дисков с моментами инерции масс

укрепленных на стальном валу с жестокостями

(рис. 28,б).

Уравнения движения системы, составленные прямым методом, таковы:

Решение системы ищем в виде

После подстановки получаем систему однородных алгебраических уравнений:

Приравнивая определитель системы нулю и раскрывая его, получим частотное уравнение

Собственные частоты колебаний:

Нулевая частота соответствует повороту вала и дисков как жесткого целого.
Для ненулевых частот определяем собственные формы колебаний, принимая А2 = 1.
Соотношение между амплитудами:

Первая форма колебаний при

Вторая форма колебаний при

Пример 10. Методом последовательных приближений определить две низших частоты собственных колебаний судовой дизельной установки по уточненной схеме, состоящей из дисков 1-6, к которым приведены кривошипы двигателей, маховика 7 и гребного винта 8 с присоединенными массами гребного вала и воды (рис.31,а) при следующих данных:

Значения частот в первом приближении определить для упрощенной трехдисковой схемы (рис. 31,б).

Рис. 31

Для приближенного определения двух низших частот образуем упрощенную схему (рис.31,б), в которой первые шесть дисков заменены одним общим, причем

Длина участка

в упрощенной схеме в 3,5 раза больше длины каждого участка между дисками 1-6 в исходной схеме, поэтому жесткости участков вала в упрощенной схеме

Таблица 1

№ диска	I		A			C
1	0,28	144,48	1,000	144,48	144,48	2.104	0,007
2	0,28	144,48	0,993	143,47	287,95	2.104	0,014
3	0,28	144,48	0,979	141,45	429,40	2.104	0,021
4	0,28	144,48	0,958	138,34	567,74	2.104	0,028
5	0,28	144,48	0,930	134,31	702,05	2.104	0,035
6	0,28	144,48	0,895	129,29	831,34	2.104	0,042
7	8,4	4334,4	0,853	3699,12	4530,46	1,2.103	3,775
8	3,0	1548,0	-2,922	-4523,85	6,61

В соответствии с (70) частотное уравнение для упрощенной схемы имеет вид

Приближенные значения двух низших частот:

В качестве первого приближения для уточнения первой собственной частоты колебаний принимаем

. Результаты расчетов представлены в табл. 1.
Полученное значение остатка

= 6,61 означает, что принятое в первом приближении значение

незначительно отличается от истинного, поэтому во втором приближении принимаем:

. Результаты расчетов сведены в табл. 2.
Таблица 2

№ диска	I		A			C
1	0,28	148,4	1,000	148,4	148,4	2.104	0,007
2	0,28	148,4	0,993	147,3	295,7	2.104	0,015
3	0,28	148,4	0,978	145,2	440,9	2.104	0,022
4	0,28	148,4	0,956	141,9	582,8	2.104	0,029
5	0,28	148,4	0,927	137,6	720,4	2.104	0,036
6	0,28	148,4	0,891	132,2	852,6	2.104	0,043
7	8,4	4452,0	0,848	3776,9	4629,5	1,2.103	3,858
8	3,0	1590,0	-3,01	-4785,8	-156,3

Частотное уравнение (75) после подстановки в него заданных числовых значений принимает вид

Собственные частоты:

Для определения собственных форм колебаний воспользуемся формулой (76)

Собственные формы колебаний представлены на рис. 34,а,б.

Рис. 34
Первая форма представляет собой, в основном, «подпрыгивание» кузова, а вторая - «галопирование».
Убедимся в ортогональности этих форм. Условие ортогональности имеет вид

Частота возмущающей силы:

При наступлении резонанса

, т.е.

,
отсюда находим длину балки при резонансе:

Для выполнения условия

двигатель нужно расположить на расстоянии:

Амплитуда вынужденных колебаний:

где

прогиб от статического действия силы

Статический прогиб от собственного веса двигателя:

Статическое напряжение:

.
Динамический коэффициент:

.
Динамическое напряжение:

Пример 13. К валу переменного сечения с жёстко заделанными концами прикреплён маховик, на который действует переменный момент

(рис.46,б). Определить максимальные касательные напряжения в левой и правой частях вала, если

коэффициент сопротивления

Массой вала пренебречь.
а

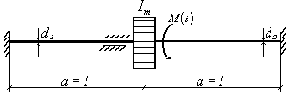
Рис. 46

Жёсткость вала:

Собственная частота колебаний:

Угол поворота маховика от действия момента, равного амплитуде возмущающего момента:

.
Амплитуда колебаний:

Соответствующий динамический момент:

Максимальные касательные напряжения в левой и правой частях вала:

Пример 14. Вдоль пути синусоидального профиля

(рис.47) с постоянной горизонтальной скоростью V движется колесо, на котором упруго подвешен груз массой m. Определить наибольшее допустимое значение коэффициента жёсткости подвески С, если требуется, чтобы амплитуда абсолютных колебаний груза не превышала

Рис. 47

Подставляя в уравнение профиля пути

, найдём ординаты нижнего конца пружины в функции времени:

Обозначая через у абсолютное вертикальное перемещение груза, отсчитываемое от равновесного уровня, дифференциальное уравнение движения запишем в виде

или

.
Отсюда следует, что эквивалентная вынуждающая сила

,
т.е. её амплитуда равна

.
Амплитуда абсолютных колебаний груза:

.
По условиям задачи

, следовательно,

< 0.5,
тогда
c <

.
Пример 15. Двигатель весом 2,4 т установлен на десяти одинаковых пружинах диаметром

. Диаметр сечения витка пружины

; модуль сдвига материала пружины

; частота вращения двигателя

. Определить число витков пружины, необходимое для того, чтобы динамический коэффициент установки был равен 0,2.

Отношение

определим, используя поставленное в условиях задачи ограничение:

.
Частота возмущающей силы:

.
Необходимое значение собственной частоты:

.
Необходимая жёсткость всех пружин:

.
Число витков:

.
Следует принять, по крайней мере, 17 витков, так как увеличение числа витков снижает жёсткость системы и уменьшает динамический коэффициент. Если принять

, то динамический коэффициент окажется больше, чем задано в условиях задачи.
Пример 16. На двух балках посередине пролёта установлен двигатель массой

. Балки (двутавр №20) имеют шарнирное опирание по концам. Ротор двигателя массой

имеет эксцентриситет

. Определить, при какой частоте вращения наступает резонанс и чему равно при этом нормальное максимальное напряжение. Коэффициент сопротивления

; длина пролёта

;

. Учесть массу балок.

Приведенная масса системы:

,
где

погонная масса балки.
Собственная частота колебаний:

.
Принимая

, находим частоту вращения двигателя при резонансе:

.
Статический прогиб от амплитудного значения возмущающей нагрузки:

;

.
Амплитуда колебаний:

.
Статический прогиб:

.
Статическое напряжение:

.
Динамическое напряжение:

.

Уравнение движения масс:

Решение уравнений ищем в виде

После подстановки получим систему алгебраических уравнений

Единичные эпюры моментов, необходимые для вычисления коэффициентов

представлены на рис.53,б,в.
Перемножая соответствующие эпюры по способу Верещагина, получим значения перемещений

Частота вибрационной нагрузки:

После подстановки в систему алгебраических уравнений находим амплитуды колебаний:

Рис. 53
Соответствующие динамические нагрузки

и Fg2 определяем из системы уравнений

Так как А1 и А2 близки по величине, то

м,
тогда

кн.
С учетом статической нагрузки находим

кн.
Максимальное напряжение в балках:

.
Пример 18. Построить эпюру динамических изгибающих моментов для невесомой балки пролетом l = 4м при действии возмущающей силы

(рис.54,а), если

Решение.
Опуская вид единичных эпюр(см. пример 7), приведем значения перемещений

Эпюра от амплитудного значения возмущающей силы показана на рис.54,б.
Перемножая эпюру

с эпюрами

(рис.29) находим:

Рис. 54
Собственные частоты колебаний балки вычислены ранее (пример 7) и равны:

«Исправленные» главные перемещения:

Система канонических уравнений динамического варианта метода сил для вычисления сил инерции X1 и X2 имеет вид:

После подстановки числовых значений коэффициентов получим:

Силы инерции:

Используя формулу:

строим эпюру динамических изгибающих моментов Mдин (рис.54,в).
Пример 19. Построить эпюру динамических изгибающих моментов в симметричной раме (рис.55,а) при действии на нее симметричной динамической нагрузки

Частота возмущающих сил

Сосредоточенные массы одинаковы и располагаются посредине каждого стержня.
Решение.
Так как вибрационная нагрузка симметрична, то формы вынужденных колебаний также будут симметричными. Групповые симметричные неизвестные силы инерции показаны на рис.55,б. Эпюры моментов от единичных сил

, действующих по направлению сил инерции, показаны на рис.55,в,г,д.

Точное значение низшей частоты такой консоли вычислено Кирхгофом в виде

.
Для приближенного решения принимаем

Каждый член этого разложения удовлетворяет граничным условиям задачи

при х=

.
Если ограничиться одним членом разложения, то по методу Рэлея

,
при этом ошибка составляет около 3 %.
Чтобы получить лучшее приближение, возьмем два члена разложения, подставив их в (274),

.
Дифференцируя это выражение по С1 и С2 поочередно, приходим к системе уравнений

.
Приравнивая нулю определитель, составленный из коэффициентов этих уравнений, получим частотное уравнение, меньший корень которого

,
что даёт ошибку 0,1 %.

Решение уравнений движения для простейшей системы

Вернёмся к рассмотрению простейшей системы - с двумя степенями свободы (рис. 22,а), на примере которой проследим получение решения уравнений движения.

Будем искать решение уравнений (32) в виде

(40)

Функции (40) не являются общим решением уравнений (32), но позволяют его построить.

Подставляя (40) в (32), получим

или

(41)

Однородная система (41) имеет тривиальное решение

, которое означает отсутствие колебаний и интереса не представляет. Ненулевое решение система (41) имеет тогда и только тогда, когда определитель, составленный из коэффициентов при амплитудах колебаний

, равен нулю:

Этот определитель называется частотным, а раскрывая его, получим частотное, или вековое уравнение

. (42)

Это частотное уравнение всегда имеет два вещественных и положительных решения, т.е. система с двумя степенями свободы (рис. 22,а) имеет две собственные частоты:

(43)

Таким образом, колебательный процесс оказывается двухчастотным и определяется функциями

. Чтобы отразить в общем решении обе гармоники, усложним индексацию и запишем решение (40) несколько в ином виде

(44)

где у амплитуды

индекс i означает номер координаты, а индекс j - номер частоты.

Установим связь между амплитудами

, используя любое из двух уравнений (41), например, первое:

. (45)

Подставим в (45) первую собственную частоту

и перейдём к двухиндексному обозначению амплитуд (см. выше), тогда получим независящее от начальных условий отношение амплитуд первой гармоники:

. (46)

Аналогично из того же соотношения (45) при

получим для

второй гармоники:

. (47)

Следовательно, решение (44) с учётом (46) и (47) можно переписать в виде

(48)

В (48) собственные частоты

и отношения

зависят только от параметров колебательной системы.
Величины

можно определить из четырёх началь ных условий, выражающих значения смещений и скоростей обеих масс в начальный момент времени.
Пусть, например, при

;

,
т.е. движение системы вызвано мгновенным ударом по второй массе.
Из (48) получим

Отсюда находим

Величины

можно вычислить по (43), (46) и (47).
Искусственным подбором начальных условий можно добиться одночастотности колебаний. Например, если сделать так, чтобы

, то колебания будут описываться одной гармоникой:

Коэффициент

не зависит от начальных условий, поэтому рассматриваемые одночастотные колебания характеризуются вполне определённым, зависящим только от параметров системы, отношением амплитуд, которое остаётся неизменным в процессе колебаний. Это отношение определяет первую собственную форму колебаний.
Если начальные условия таковы, что

, то колебания будут также одночастотными, но с частотой

при этом отношение амплитуд

определяет вторую собственную форму колебаний.

Решение уравнений движения в общем случае

Частное решение системы уравнений (31) можно записать в виде

(36)

Этими выражениями описывается моногармонический колебательный режим с частотой

, общей для всех координат

Подставляя (36) в (31), получим систему алгебраических уравнений:

(37)

Система (37) является однородной; амплитуды

не могут одновременно равняться нулю, следовательно, ненулевому решению системы соответствует равенство нулю определителя:

(38)

Для системы с двумя степенями свободы частотное уравнение оказывается биквадратным:

(39)

Если положить здесь

, то корни частотного уравнения

;

называются парциальными частотами.

Можно доказать, что парциальные частоты больше меньшей частоты

заданной системы и меньше её большей частоты

. Отсюда следует, что связь между выбранными обобщёнными координатами, выраженная параметрами

, "раздвигает" значения собственных частот.

Силовое возбуждение колебаний

Независимо от природы вынуждающих сил будем исходить из того, что каждая из них задана в виде некоторой функции времени

где

1,2,...,n - порядковый номер материальной точки.

Рассмотрим простейшую систему (рис.35,а) с одной степенью свободы, которая совершает колебания под действием вынуждающей силы F(t). В любой момент времени на груз массой m действуют две силы: сила упругости пружины, пропорциональная смещению груза X, и возмущающая сила F(t), изменяющаяся во времени по некоторому, заранее заданному закону (рис.35,б).

Рис. 35

Дифференциальное уравнение движения груза:

где С - жесткость пружины,

или

(81)

Это уравнение иногда называют стандартным, так как к нему можно прийти и при рассмотрении других систем с одной степенью свободы, имеющих совершенно иной конструктивный вид.

В качестве примера рассмотрим задачу о колебаниях, вызываемых единичным толчком, т.е. внезапно приложенной в момент времени

и затем постоянно действующей силой F = 1 (рис. 36,а).

При

дифференциальное уравнение движения имеет вид

Решение уравнения должно удовлетворять начальным условиям

при

и представляет собой сумму общего решения соответствующего однородного уравнения

и частного решения заданного уравнения

т.е.

Используя начальные условия, определим постоянные интегрирования С1 и С2:

и тогда

Этот закон движения показан на рис. 36,б. Максимальное значение смещения x составляет

, т.е. в два раза превышает перемещение, вызванное статическим действием силы F = 1.

Рис. 36

Случаи периодического изменения параметрических нагрузок

Простейший пример рассматриваемого типа представлен на рис.60,а.

Масса 1 закреплена на верхнем конце вертикального абсолютно жесткого стержня 2; внизу стержень имеет опору, упруго сопротивляющуюся повороту опорного сечения («упругий шарнир»). На верхний конец стержня действует вертикальная сила F. Такая система представляет собой результат упрощенной схематизации реального стержня, обладающего распределенными массой и упругостью.

Сила F является параметрической нагрузкой, и если она постоянна во времени, ее критическое значение можно найти при помощи формулы Эйлера.

Рис. 60

Пусть

- угол отклонения стержня от вертикали; C - коэффициент жесткости упругого шарнира. Тогда восстанавливающий момент (момент упругого шарнира) составляет -

, а уравнение имеет вид

(156)

Очевидно, что

; отсюда следует, что отклоненное состояние равновесия возможно, если

(157)

Этой формулой определяется критическое значение статически действующей силы F (например веса груза 1).

Это же значение можно найти, рассматривая свободные колебания груза 1. В отличие от уравнения статики (156) уравнение моментов относительно шарнира 3 содержит инерционное слагаемое:

(158)

или

При

частота свободных колебаний системы обращается в нуль, т.е. система становится неустойчивой. Значение критической силы вновь определяется формулой (157).

Рассмотрим случай, когда сила F изменяется во времени, следуя гармоническому закону:

При этом уравнение колебаний стержня (158) принимает вид

или

Это уравнение приводится к стандартной форме - уравнению Матье (151), если положить

(159)

При возрастании частоты

параметры

пропорционально уменьшаются. Штриховой луч (рис.58) указывает, что система проходит ряд последовательно чередующихся устойчивых и неустойчивых состояний. Наклон луча определяется отношением

где

-статическая критическая сила, определяемая выражением (157).

При данном значении

величина

зависит от разности

. Чем ближе значение статической составляющей

к критическому значению

, тем круче проходит луч и тем шире пересекаемые им участки областей неустойчивости.

Потеря устойчивости возможна при сколь угодно малых значениях сжимающей статической составляющей

и даже при изменении ее знака, т.е. при растягивающей статической составляющей. Как видно из рис. 58, луч

при

< 0 проходит весьма полого, но также пересекает ряд областей неустойчивости.

С другой стороны, диаграмма Айнса-Стретта позволяет установить, что устойчивость системы возможна при

и даже при

. Действительно, если

, то

луч

совпадает с осью ординат диаграммы Айнса-Стретта, но система остается неустойчивой, если

Согласно условиям (159), для этого необходимо выполнение неравенства

При

луч

располагается во втором квадранте диаграммы; из рис.60,б следует, что и в этом случае возможна устойчивость системы в надлежаще выбранном диапазоне изменения частот

. Таким образом, вибрационная составляющая сжимающей силы может при определенных условиях стабилизировать систему, которая неустойчива в отсутствие колебаний.

Случаи периодического изменения жесткости

В качестве примера рассмотрим систему, упругой частью которой является зубчатый (шлицевой) вал 1 (рис.59,а). На нижнем конце вала находится диск 2. С валом соединена зубчатая (шлицевая) массивная втулка 3, которая может скользить вдоль оси вала и совершать гармонические колебания в вертикальном направлении. В этой системе возможно возбуждение не только изгибных, но и крутильных колебаний. Пусть свободная длина вала в текущий момент времени t составляет

Коэффициент жесткости вала на кручение:

(155)

Рис. 59

Если амплитуда колебаний А значительно меньше среднего значения длины

, то (155) можно представить в виде

что по структуре совпадает с (152), следовательно, крутильные колебания рассматриваемой системы также описываются уравнением Матье (151), причем

При некоторых условиях, определяемых диаграммой Айнса-Стретта, рассматриваемая система может оказаться в состоянии параметрического резонанса.

Другим примером параметрического возбуждения колебаний при периодическом изменении жесткости является система, изображенная на рис.59,б. Шахтная клеть 1 равномерно движется по вертикальным направляющим 2, которые закреплены на шпалах 3. В этой системе поперечная жесткость, определяющая восстанавливающую упругую силу при поперечных колебаниях клети, есть величина переменная: если клеть находится на уровне очередной пары шпал, то эта жесткость достигает максимума, если же клеть расположена против середины свободного пролета направляющих, то жесткость минимальна. Частота изменения жесткости зависит от расстояния между шпалами и от скорости движения клети:

а отсюда следует, что существует ряд «запретных» диапазонов скорости V, соответствующих условиям параметрического резонанса. Эти соображения полностью подтверждены экспериментальными исследованиями.

Стержневые системы с конечным числом степеней свободы при гармоническом нагружении

При действии на упругую систему (балку или раму) с конечным числом степеней свободы вибрационной гармонической нагрузки изгибающие моменты, поперечные и продольные силы также будут изменяться во времени, а их наибольшие значения (амплитуды) будут зависеть от частот возмущающих сил. Если все возмущающие нагрузки, действующие на систему, имеют одну и ту же частоту р и изменяются в одной фазе, то силы инерции, а следовательно, и изгибающие моменты, поперечные и продольные силы достигают наибольших значений в одно и то же время.

Для решения задачи о вынужденных колебаниях стержневой системы можно использовать как метод сил, так и метод перемещений, причём наибольшее применение в расчётной практике находит первый из указанных методов.

Метод сил. Рассмотрим упругую систему (рис.50) с конечным числом сосредоточенных масс, на которую действуют вибрационные силы

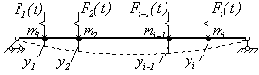
Рис. 50

Перемещение любой массы

в произвольный момент времени

выражается в виде

, (135)

где

силы инерции соответствующих масс;

перемещения по направлению силы инерции

, вызванные единичными силами

, приложенными в точках нахождения соответствующих масс;

перемещение точки расположения массы

от действия амплитудных значений всех приложенных вибрационных нагрузок.

Перечисленные перемещения вычисляются путём перемножения соответствующих эпюр методом Мора-Верещагина.

С другой стороны, при гармонических вынужденных колебаниях с

частотой р перемещение массы

и её ускорение можно записать в виде

Сила инерции массы

отсюда

(136)

Подставляя (136) в (135), после простейших преобразований получим

где

Записывая аналогичные уравнения для каждой из сосредоточенных масс, получим систему уравнений, которая называется системой канонических уравнений динамического варианта метода сил:

(137)

где

число степеней свободы системы.

Уравнения (137) позволяют определить наибольшие (амплитудные) значения сил инерции.

Сама система уравнений (137) по форме аналогична системе канонических уравнений метода сил, используемого при расчёте статически неопределимых систем, но неизвестными в ней являются не реакции отброшенных связей в статически неопределимой системе, а амплитуды сил инерции масс, которые могут возникать как в статически определимой, так и в статически неопределимой системах.

После вычисления максимальных значений сил инерции

эпюра динамических изгибающих моментов строится путём сложения единичных эпюр, предварительно умноженных на найденные значения соответствующих инерционных сил, с эпюрой

, т.е. в соответствии с выражением

.

Использование симметрии системы при её расчёте на вынужденные колебания оказывается возможным только при симметричном расположении масс.

Рис. 51

При несимметричной вибрационной нагрузке разложение сил инерции на симметричные и обратно симметричные группы (рис.51) приводит к распаду системы канонических уравнений на две независимые системы.

В этом случае вычисление главных перемещений по направлению парных неизвестных нужно вести по формуле

.

При симметричной вибрационной нагрузке все обратно симметричные силы инерции равны нулю, а при обратно симметричной вибрационной нагрузке симметричные силы инерции равны нулю. Симметричная нагрузка может привести к резонансу только при совпадении её частоты с собственными частотами симметричных колебаний системы и, наоборот, обратно симметричная нагрузка может дать резонанс только с частотами обратно симметричных свободных колебаний.

Метод перемещений. Этому методу отдают предпочтение при расчёте рам на вынужденные колебания. Рассмотрим систему (рис.52,а), для которой основная система получается путём введения связей по направлению неизвестных перемещений

соответствующих масс

(рис.52,б).

а б

Рис. 52

Уравнение, выражающее равенство нулю динамической реакции введённой связи по направлению любого перемещения

с учётом силы инерции

, выражается в виде

.

Учитывая, что при гармонических колебаниях

, получим систему уравнений

(138)

где

.

Строго говоря, неизвестные

и свободные члены

являются величинами переменными, изменяющимися одновременно и по одному и тому же закону, характеризуемому множителем

, к их амплитудным значениям. Так как этот множитель присутствует во всех членах системы (138), то на него может быть произведено сокращение. Тогда неизвестные и свободные члены уравнений (138) должны рассматриваться в качестве соответствующих амплитудных значений.

Реакции

определяются от единичных перемещений основной системы, приложенных в тех сечениях, где находятся точечные массы, т.е. так же, как и при определении частот свободных колебаний.

Реакции от амплитудных значений вибрационных нагрузок

определяются в основной системе.

После вычисления неизвестных амплитуд перемещений

эпюра динамических изгибающих моментов строится в соответствии с выражением

,

где

эпюры изгибающих моментов в основной системе от соответствующих единичных перемещений;

эпюра моментов в основной системе от амплитудных значений вибрационных нагрузок.

Система уравнений (138) по своей структуре аналогична системе канонических уравнений метода перемещений, применяемого для расчёта статически неопределимых систем, но здесь неизвестные

являются не искомыми перемещениями узлов рамы, а амплитудами перемещений сосредоточенных масс.

Так же как и метод сил, метод перемещений может быть использован не только для систем, совершающих изгибные вынужденные колебания, но и для систем, испытывающих продольные вынужденные колебания.

Сухое трение

Рассмотрим движение упруго закрепленного тела массой m по шероховатой поверхности. Как уже отмечалось, в этом случае говорят, что имеет место сухое трение (рис.17). Сила трения, действующая на массу m, постоянна по величине и направлена в сторону, противоположную движению. Уравнение свободных колебаний такой системы имеет вид

, (24)

где знак плюс соответствует этапу движения, на котором скорость положительна, а знак минус - этапу движения, на котором скорость отрицательна.

Зависимость полной действующей на груз силы F=cx

R0 от смещения x показана на рис. 18,а.

Рис. 17

Перепишем уравнение (24) в виде

. (25)

Функция sgn

есть единичная функция, имеющая знак аргумента (рис. 18,б); sgn

=1 при

>0; sgn

=-1 при

<0; sgn=0 при

=0.

Уравнение (25) содержит нелинейное слагаемое. Тем не менее можно найти решение, если рассмотреть последовательные интервалы движения, на каждом из которых скорость

имеет постоянный знак.

Отклоним массу m в крайнее правое положение на величину А и отпустим ее без начальной скорости. В этом случае

x0=A ;

. (26)

Под действием натяжения пружины на этом этапе груз двигается влево (

<0) и уравнение движения

или

, (27)

где

;

Коэффициент а представляет собой отклонение груза под действием максимально возможной силы трения. При отклонении массы m на величину, меньшую или равную а, движение не начнётся, так как силы упругости пружины недостаточно для преодоления силы трения. Полоса -а<x<a называется зоной застоя. Поэтому уравнение (27) имеет место при А>a.

Рис. 18

Общее решение уравнения (27) имеет вид

Определяя постоянные интегрирования из начальных условий (26) получим

. (28)

Закон движения (28) справедлив до тех пор, пока

<0. Так как

, то скорость движения будет отрицательной до момента времени t1, определяемого из условия:

.
В этот момент масса m остановится, смещение x равно

,

т. е. под влиянием трения отклонение массы m уменьшилось по абсолютной величине на 2а.

После остановки масса m начнёт двигаться вправо. Повторяя приведенные выше расчёты, можно показать, что движение слева направо также продолжается в течение времени

. Максимальное отклонение вправо равно А-4а. Процесс движения будет продолжаться до тех пор, пока масса m не остановится в зоне застоя. Зависимость смещения x от времени t на каждом этапе движения представляет собой косинусоиду, смещённую по оси x на величину а или -а, с амплитудой, уменьшающейся по закону арифметической прогрессии (рис.18*).

Рис. 18*

Время

между двумя соседними максимумами отклонения, которое условно можно назвать периодом колебаний,

.

Наличие сухого трения не меняет частоту колебаний.

Фазовый портрет свободных колебаний системы с сухим трением представлен на рис.19.

В координатах

гармонический закон движения изображается дугами окружностей.

Если в (27) ввести новую переменную

, то получится уравнение гармонических колебаний без трения. Это движение на фазовой плоскости изображается полуокружностью радиусом

с центром в точке

. На втором этапе движения, когда

, уравнение движения

может рассматриваться как уравнение гармонических колебаний со смещением

. На фазовой плоскости на втором этапе движения получаем полуокружность с центром в точке

. И так до тех пор, пока кривая при

не попадёт в зону застоя

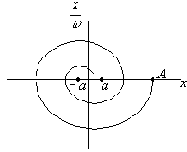
Рис. 19

Свободные колебания автомобиля

Рассмотрим автомобиль как систему упругосвязанных между собой жестких тел (рис. 32,а). Здесь тело 1 схематически представляет собой кузов автомобиля, тела 2-5 - колеса, массы которых будем считать сосредоточенными.

Движение такой системы в процессе колебаний характеризуется семью координатами:

- вертикальное перемещение центра тяжести кузова;

- вертикальные перемещения центров тяжести колес;

- угол поворота кузова относительно поперечной оси;

- угол поворота кузова относительно продольной оси.

Распределение масс автомобиля и жестокостей упругих связей почти симметрично относительно средней продольной плоскости, поэтому в расчетах колебаний некоторой малой асимметрией можно пренебречь. При этом общий процесс колебаний можно рассматривать состоящим из двух взаимно не связанных процессов (рис. 32,б,в): продольных колебаний, характеризуемых вертикальным перемещением кузова

, поворотом кузова вокруг поперечной оси

и попарно равными перемещениями обоих передних колес

и обоих задних колес

; поперечных (боковых) колебаний, характеризуемых поворотом кузова вокруг продольной оси

и попарно равными перемещениями обоих левых колес

и обоих правых колес

Рис. 32

В соответствии с этим продольные колебания описываются четырьмя, а поперечные колебания - тремя дифференциальными уравнениями.

Рассмотрим продольные колебания, которые имеют основное значение.

Обозначим жесткости шин через С; жесткости передних и задних рессор через СП и СЗ соответственно; массы кузова и колеса - через m и mК. Радиус инерции кузова относительно поперечной оси, проходящей через его центр тяжести, обозначим через

Тогда деформации рессор составляют

(передняя рессора);

(задняя рессора).

Уравнения движения составим на основе уравнений Лагранжа.

Кинетическая энергия системы складывается из следующих частей:

кинетической энергии кузова

;

кинетической энергии передних колес

;

кинетической энергии задних колес

Суммарная кинетическая энергия:

Потенциальная энергия деформации рессор:

.

Потенциальная энергия сжатия шин:

.

Суммарная потенциальная энергия:

.

Вычисляя соответствующие производные и подставляя в уравнения Лагранжа (29), получим

(73)

Частное решение системы (73) имеет вид

Подстановка частного решения в уравнение (73) приведет, как в рассмотренных ранее системах, к однородным относительно амплитуд

алгебраическим уравнениям и соответственно обнаружатся четыре собственных частоты колебаний.

С практической точки зрения удовлетворительный результат дает рассмотрение упрощенной схемы продольных колебаний (рис. 32,г).

Будем считать шины недеформируемыми, тогда рассматриваемая система обладает двумя степенями свободы, соответствующими координатам

. Положим в полученных выше выражениях для кинетической и потенциальной энергий

, тогда эти выражения принимают вид

Уравнения Лагранжа:

Частное решение

После его подстановки получим

или

(74)

Как обычно, для получения нетривиального решения приравниваем нулю определитель системы:

Раскрывая определитель, получим частотное уравнение в виде

(75)

Определив из уравнения (75) собственные частоты, можно найти соответствующие им собственные формы колебаний. Для этого из какого-либо (например, из первого) уравнения системы (74) нужно образовать отношение амплитуд

(76)

и подставить в него поочередно оба корня частотного уравнения.

Рассмотрим подробно частный случай такого распределения масс, при котором

В этом случае частотное уравнение (75) имеет корни:

(77)

Для определения собственных форм колебаний подставим эти корни поочередно в соотношение (76). Тогда для первой собственной формы получим

а для второй собственной формы -

Эти формы колебаний представлены на рис. 33,а,б. Их особенностью является неподвижность одной оси автомобиля при колебаниях другой. Формулы (77) показывают, что в этом частном случае частоты можно вычислять, используя схему, показанную на рис.33,в, т.е.

распределяя общую массу по закону рычага.

Рис. 33

В другом частном случае, когда Спа = СЗb, уравнения (74) становятся независимыми

(78)

что означает возможность чисто вертикальных колебаний при отсутствии поворотов - «подпрыгивание» (рис. 33,г), а также чисто угловых колебаний при неподвижности центра тяжести - «галопирование» (рис. 33,д). Действительно, система (78) удовлетворяется решением

при выполнении равенства

(79)

и решением

при выполнении равенства

(80)

Из (79) находим первую собственную частоту:

,

а из (80) - вторую собственную частоту:

.

Пример 11. Определить собственные частоты и собственные формы колебаний автомобиля, для которого известно:

Свободные колебания систем с конечным числом степеней свободы (общий случай)

Как уже говорилось (см. подразд. 1.4), дифференциальные уравнения движения таких систем можно получить тремя основными способами: 1) в форме уравнений Лагранжа; 2) прямым способом; 3) обратным способом.

Наиболее общий вид дифференциальных уравнений движения может быть получен в форме уравнений Лагранжа

, (29)

где K и П - кинетическая и потенциальная энергии соответственно;

- обобщённые координаты и обобщённые скорости;

число степеней свободы системы.

Известно, что при малых колебаниях около положения равновесия кинетическая и потенциальная энергии выражаются через обобщённые координаты и обобщённые скорости следующим образом:

;

, (30)

где

инерционные коэффициенты;

квазиупругие коэффициенты, называемые также обобщёнными коэффициентами жёсткости.

Подставляя (30) в (29), получим систему однородных линейных дифференциальных уравнений с постоянными коэффициентами:

(31)

Однако составление уравнений движения по схеме Лагранжа не является обязательным, потому что во многих случаях прямой или обратный способы оказываются более удобными.

Рассмотрим особенности названных способов на примере системы с двумя степенями свободы, состоящей из тел с массами

,соединённых пружинами с жесткостями

(рис. 22,а).

За обобщённые координаты примем горизонтальные перемещения

грузов, отсчитываемые от положения равновесия, в которых отсутствуют деформации пружин. Удлинения пружин в процессе движения:

;

Основной способ (уравнения Лагранжа)

Кинетическая энергия рассматриваемой системы:

Потенциальная энергия деформации пружин:

Вычислим производные, необходимые для подстановки в уравнения Лагранжа:

;

Подставляя вычисленные значения в (29), получим дифференциальные уравнения движения рассматриваемой системы

(32)

Прямой способ

Выделяем массы

и рассматриваем их как свободные тела под действием сил упругости, определяемых удлинениями

обеих пружин (рис. 22,б):

Дифференциальные уравнения движения грузов имеют вид

Подставляя значения

, получим

т.е. эти уравнения совпали с уравнениями (32).

а б

Рис. 22

Свободные колебания систем с распределёнными параметрами

Основная особенность процесса свободных колебаний систем с бесконечным числом степеней свободы выражается в бесконечности числа собственных частот и форм колебаний. С этим связаны и особенности математического характера: вместо обыкновенных дифференциальных уравнений, описывающих колебания систем с конечным числом степеней свободы, здесь приходится иметь дело с дифференциальными уравнениями в частных производных. Кроме начальных условий, определяющих начальные смещения и скорости, необходимо учитывать и граничные условия, характеризующие закрепление системы.

Свободные колебания системы с одной степенью свободы без трения

В большинстве упругих систем при достаточно малых перемещениях сила упругости линейно зависит от перемещения x. Если начало отсчёта смещения x выбрать так, что при x=0: F=0, то для линейной системы F = cx, где с - коэффициент жесткости системы.

Дифференциальное уравнение движения системы с одной степенью свободы (рис. 11,а) таково:

. (4)

Вид дифференциального уравнения не меняется при действии на систему постоянных сил (например, сил тяжести), если смещение тела отсчитывать от положения его статического равновесия.

Рис. 11

Действительно, уравнение движения тела массой m (рис.11,а), находящегося под действием силы тяжести и совершающего свободные колебания, имеет вид

, (5)

где

- удлинение пружины от силы тяжести груза.

Следовательно, слагаемые mg и cfст в уравнении (5) взаимно уничтожаются, и уравнение (5) совпадает с (4).

Уравнение движения одномассовой системы, совершающей крутильные свободные колебания (рис. 11,б), записывается аналогично:

где

- угол поворота тела; J- момент инерции массы m относительно продольной оси вала; с - крутильная жесткость упругой связи.

Решение уравнения (4) имеет вид

, (6)

где

- угловая частота колебаний, или собственная частота; С1 и С2- постоянные интегрирования, определяемые из начальных условий.

Обозначая смещение и скорость в начальный момент времени t0=0 через x0 и

соответственно, после подстановки в (6) находим

. (7)

Выражение (6) можно записать иначе:

, (8)

где

Таким образом, движение груза при свободных колебаниях одномассовой системы без трения описывается синусоидальным законом с амплитудой колебаний А, периодом

и начальной фазой

(рис.12).

Период колебаний

определяется из условия:

откуда

. (9)

Число колебаний в единицу времени (техническая частота, измеряемая в герцах):

. (10)

Рис. 12

В практическом отношении иногда оказывается удобным связать частоту и период колебаний со статической деформацией fст упругой связи, вызванной силой, равной весу груза,

.

При этом справедливы формулы:

;

. (11)

Так как величина fст введена в (11) формально, то очевидна их справедливость независимо от того, совпадает или не совпадает направление силы тяжести с направлением движения груза.

Для анализа свободных колебаний удобно использовать изображение закона движения системы на фазовой плоскости, или так называемый фазовый портрет. Фазовым портретом движения называется графическое изображение зависимости скорости движения от смещения. Для получения фазового портрета продифференцируем выражение (8) по t:

(12)

Уравнение движения (8) и выражение (12) представляют собой уравнение фазовой траектории в параметрической форме. Исключая параметр

, получим

. (13)

Уравнение (13) является уравнением эллипса с полуосями, равными А и

(рис. 13,а). Верхняя полуплоскость соответствует возрастанию смещения, нижняя - убыванию. Размеры эллипса зависят от начальных условий, определяющих амплитуду колебаний А.

Рис. 13

Все возможные свободные колебания одномассовой системы изображаются семейством эллипсов, каждый из которых соответствует определённому уровню энергии. Чем больше амплитуда колебаний А, тем больше полная энергия системы. Если значения энергии откладывать по оси , перпендикулярной чертежу, то получится поверхность (параболоид), нижняя точка которой соответствует нулевому энергетическому уровню. Точка, изображающая значения смещения и скорости в данный момент времени (изображающая точка), перемещается по горизонтали этой поверхности.

Если изменить масштаб построения фазовой траектории и откладывать по оси абсцисс х, а по оси ординат -

, то фазовая траектория (рис. 13,б) будет представлять собой окружность радиусом А, причём изображающая точка будет равномерно двигаться по этой окружности с угловой скоростью, равной частоте собственных колебаний

.

При наличии рассеяния энергии изображающая точка перемещается по спирали, приближаясь к началу координат.

Свободные колебания стержневых систем

С изгибными свободными колебаниями многомассовых стержневых систем часто приходится сталкиваться в строительных конструкциях, а также в турбинах, где применяют валы с прямолинейной осью, несущие ряд дисков.

В качестве примера такой системы рассмотрим шарнирную балку с тремя сосредоточенными массами

(рис. 25,а).

Для таких систем при составлении уравнений движения удобнее использовать обратный способ, основанный, как уже говорилось, на введении сил инерции, приложенных к безмассовому упругому "скелету" системы. При этом удобно использовать понятие единичного перемещения

как перемещения в направлении i, вызванного безразмерной единичной силой, действующей в направлении k (рис. 25,б).

Если на систему по k-му направлению действует сила

и требуется определить вызванное ею полное перемещение в i-м направлении, то вследствие пропорциональности между силой и перемещением (справедлив закон Гука) можно записать, что

. При одновременном действии сил

полное перемещение по i-му направлению определяется суммированием

а б

Рис. 25

Итак, рассмотрим свободные колебания балки, несущей сосредоточенные массы

(рис. 25,а). Развиваемые ими силы инерции

являются единственной нагрузкой на упругий "скелет" системы в процессе колебаний. Можно составить следующие выражения для перемещений точек приложения сосредоточенных масс под действием этих сил инерции:

(60)

Перемещения

вычисляются, как обычно, методами О. Мора или А.Н. Верещагина от единичных сил, приложенных в местах действия сил инерции, т.е. в сечениях, где находятся сосредоточенные массы.

Система дифференциальных уравнений (60) имеет частное решение в виде

(61)

Вторые производные этих перемещений по времени, т.е. ускорения, выражаются так:

(62)

Подставляя (61) и (62) в систему уравнений (60) и сокращая на

, после простейших преобразований получим

(63)

Отбрасывая тривиальное решение этой системы уравнений

как не отвечающее физическому смыслу рассматриваемой задачи, будем искать ненулевое решение исходя из условия равенства нулю определителя системы (63):

. (64)

Частотное уравнение, получаемое при раскрытии определителя (64) при числе степеней свободы системы

, может быть решено строго непосредственно. При

получение решения может оказаться затруднительным или даже невозможным.

Если направления перемещений

выбраны так, что побочные перемещения

обращаются в нуль, то система дифференциальных уравнений (60) и соответствующее ей уравнение частот распадаются на отдельные уравнения, содержащие только главные перемещения

. В этом случае перемещения

называются главными координатами, а соответствующие формы колебаний - главными формами колебаний.

Главные формы колебаний обособлены друг от друга и каждая из них происходит со своей определённой частотой, которая выражается формулой, аналогичной формуле для вычисления собственной частоты системы с одной степенью свободы

.

Выбор главных координат для систем с числом степеней свободы, большим двух, в общем случае весьма затруднителен. При

это возможно всегда.

Для симметричных систем с симметрично расположенными массами возможны прямо симметричные и обратно симметричные формы колебаний, при которых силы инерции будут соответственно прямо симметричны и обратно симметричны. В этом случае перемещения вычисляются как групповые от парных прямо симметричных или обратно симметричных единичных сил. Побочные перемещения, связывающие прямо симметричные и обратно симметричные силы инерции, обращаются в нуль. Это также приводит к распаду частотного уравнения на два независимых уравнения, из которых одно позволяет найти частоты прямо симметричных колебаний, а другое - обратно симметричных. Так как групповые перемещения определяются от парных единичных сил, то соответствующая масса должна входить в частотные уравнения с коэффициентом 0,5.

Теорема и метод Рэлея

Согласно этой теореме, истинное значение низшей собственной частоты всегда меньше, чем приближенное значение частоты, вычисленное энергетическим способом. Докажем эту теорему для изгибных колебаний, совершенно аналогично она доказывается и для других видов колебаний.

Положим, что при решении энергетическим способом задачи о свободных изгибных колебаниях была принята форма колебаний f = f(x). Тогда соответствующая статическая нагрузка, способная вызвать изгиб по кривой f(х), может быть представлена в виде

Следовательно, приближенное выражение для квадрата частоты

. (264)

Ввиду известного произвола в выборе функции f(x) она не совпадает ни с одной из собственных форм, которые являются точными решениями; однако функцию f(x) можно представить в виде ряда по этим формам. Если ищут низшую собственную частоту, то функцию f(x) можно представить так:

f(x) = X1(x)+ b2X2(x)+b3X3(x) +... (265)

При удачном выборе функция f(x) близка к Х1(х), поэтому коэффициенты b2 , b3 ... - малые числа .

Два раза продифференцируем выражение (265) по х, затем умножим обе части на жёсткость EJ и вновь дважды продифференцируем результат. Тогда получим

(266)

Согласно основному уравнению (243), можно записать:

;

;...

Подставляя эти значения в выражение (266), получим

(267)

При помощи (265) и (267) образуем числитель формулы (264):

Вследствие ортогональности собственных форм все интегралы от произведений, где индексы сомножителей различны, равны нулю, поэтому

. (268)

Знаменатель формулы (264) получим при помощи (265) в виде

(269)

Здесь также исчезают все члены, содержащие произведения Xm Xn. Подставляя (268) и (269) в (264), получим квадрат низшей частоты

(270)

Так как w1<w2<w3<...,то все дроби

больше единицы и, следовательно, все члены числителя, начиная со второго, больше соответствующих членов знаменателя. Поэтому вся дробь, входящая в (270), больше единицы, т е.

w2>

, (271)

что и утверждается теоремой Рэлея.

Неравенство (271) справедливо не только для изгибных, но и для продольных и крутильных колебаний.

Теория колебаний оболочек без растяжения срединной поверхности

На основе описанной выше теории рассмотрим колебания цилиндрической оболочки (рис.75). Определим положение произвольной точки

на срединной поверхности оболочки координатами

Рис.75

Компоненты перемещения точки в продольном, окружном и нормальном к поверхности направлениях обозначим соответственно

. Компоненты деформации срединной поверхности определяются формулами

(344)

Приравняв

нулю и проинтегрировав полученные уравнения, выразим

через две произвольные функции угловой координаты

(345)

Из полученных формул видно, что при деформации цилиндрической оболочки без растяжения срединной поверхности образующие остаются прямыми, а осевые перемещения не зависят от продольной координаты.

Формулы показывают, что чистые изгибания замкнутой цилиндрической оболочки возможны в следующих случаях: а) если ее торцы свободны; в этом случае отличны от нуля

; б) если на одном из торцов запрещены перемещения

, но разрешено перемещение

; в) если на одном из торцов запрещено перемещение

. Если же оболочка оперта на обоих торцах, чистое изгибание ее невозможно.

Составим выражения потенциальной и кинетической энергии оболочки, совершающей гармонические колебания с частотой

. В общем выражении потенциальной энергии деформации сохраняется только слагаемое

. Входящие в него параметры изменения кривизны определяются формулами

После подстановки этих значений в выражение

(341) и интегрирования по

с учетом того, что

, находим

(346)

где

Интегралы в выражениях

вычисляются по всей длине оболочки.

Из основного уравнения метода Рэлея-Ритца следует, что выражение

(где

- частота собственных колебаний) должно иметь стационарное значение:

Отсюда следует система обыкновенных дифференциальных уравнений для функции

. В этом случае, если форма всех меридиональных сечений одинакова (толщина оболочки не зависит от

), коэффициенты

постоянны и уравнения получают такой вид:

(347)

. (348)

Решение этих дифференциальных уравнений для открытых оболочек должно быть подчинено граничным условиям на продольных кромках.
На этих кромках могут быть заданы перемещения

(постоянные вдоль каждой кромки), а также перемещения

и угол поворота

в двух различных сечениях по длине оболочки. Всего имеется семь кинематических граничных условий на каждой продольной кромке, что соответствует четырнадцатому порядку уравнений (347)-(348). Если закрепления отсутствуют, то кинематические граничные условия заменяются естественными граничными условиями.

Если оболочка симметрична относительно поперечного сечения

(рис.76,а), то

и функции

определяются независимыми дифференциальными уравнениями

(349)

Функция

описывает в этом случае кососимметричные относительно сечения

формы колебаний, а функция

- симметричные. Уравнение, определяющее функцию

, совпадает с уравнением колебаний кольца в своей плоскости.

Рис.76

Для замкнутой оболочки граничные условия заменяются условиями периодичности, которым удовлетворяют функции

. В случае симметричной оболочки подстановка этих выражений в уравнения (349) приводит к следующим значениям частот для

кососимметричных колебаний:

и для симметричных колебаний:

.

Для оболочки постоянной толщины

и длины

(рис.76,б):

В этом случае

Как видно из полученных формул, при колебаниях оболочек без растяжения срединной поверхности частоты определяются зависимостями такого же типа, как и для пластинок

где

- цилиндрическая жесткость;

- числовой коэффициент. При стремлении толщины оболочки к нулю частота ее колебаний без растяжения срединной поверхности также стремится к нулю.

Уравнение движения пластины постоянной толщины

Расположим оси

в срединной плоскости пластины, ось

направим по нормали к этой плоскости. Дифференциальное уравнение статического изгиба пластины постоянной толщины

при малых перемещениях имеет вид

где

- бигармонический оператор;

- прогиб;

- цилиндрическая жесткость;

- интенсивность нормальной нагрузки.

Добавляя к внешней нагрузке интенсивность сил инерции,

(313)

где

- плотность материала, получим уравнение движения

(314)

При свободных колебаниях нагрузка

, и решение уравнения (314) ищется в виде

(315)

Подставляя (315) в однородное уравнение, соответствующее (314), получим для амплитудной функции

уравнение в частных производных

(316)

где

Уравнение (316) может быть представлено так:

откуда следует, что решениями (316) являются, в частности, решения более простых уравнений:

(317)

или

Из бесчисленного множества решений уравнения (316) должны быть отобраны те, которые соответствуют условиям закрепления краев пластинки. Эти условия будут такими же, как и при статическом изгибе: на жестко защемленном краю

на шарнирно опертом краю

на свободном краю

где

- амплитудный изгибающий момент и приведенная поперечная сила на контуре.

Если пластина отнесена к декартовой системе координат

то

определяются формулами

где

- угол, образуемый внешней нормалью к контуру с осью х;

- радиус кривизны контура.

Уравнения движения оболочек

Если отнести оболочку к системе гауссовых координат

, совпадающих с линиями кривизны срединной поверхности, то уравнения движения могут быть записаны в таком виде:

(350)

где

- компоненты перемещения точки срединной поверхности в направлениях

- и

-линий и по нормали;

- масса оболочки на единицу срединной поверхности;

- дифференциальные операторы. Структура операторов

для оболочек произвольной формы весьма сложна. Поэтому уравнения движения в виде (350), т.е. в перемещениях, имеет смысл записывать только для простейшего случая цилиндрической оболочки постоянной толщины, для которой коэффициенты уравнений постоянны. В этом случае

(351)

где

;

- безразмерные координаты точки на срединной поверхности;

Система уравнений (350) имеет восьмой порядок по координатам

и второй - по времени

. Даже тогда, когда эти уравнения имеют постоянные коэффициенты (т.е. для цилиндрической оболочки) и при рассмотрении гармонических колебаний с частотой

, т.е. при

аналитическое решение этих уравнений может быть получено лишь при некоторых специально подобранных граничных условиях. В остальных случаях для расчета используют приближенные или численные методы.

Особенностью уравнений движения оболочек является то, что, как это видно из формул (351), в эти уравнения входит малый, пропорциональный квадрату толщины оболочки, параметр

, на который умножаются старшие производные перемещений по координатам. Поэтому, если рассматриваются такие формы колебаний, при которых перемещения медленно меняются по координатам

, соответствующими моментными членами в уравнениях (350) можно пренебречь. На основе безмоментной теории рассматривают низшие формы колебаний оболочек, закрепленных так, что обеспечивается возможность безмоментного состояния.

При высших формах собственных колебаний оболочка разбивается узловыми линиями на ряд достаточно пологих сегментов, на каждом из которых напряженное состояние быстро изменяется по координатам. В этом случае для расчета может быть использована так называемая теория пологих оболочек.
Применительно к цилиндрической оболочке уравнения теории пологих оболочек получаются из уравнений (350), если в операторах

(351) опустить слагаемые с множителем

.

Аналитическое решение задачи о собственных колебаниях для замкнутой цилиндрической оболочки может быть получено при так называемых граничных условиях Навье. Согласно этим условиям, на торцах оболочки отсутствуют нормальные

и окружные

перемещения, а также продольная сила

в срединной поверхности и изгибающий момент

. Условиям Навье удовлетворяют следующие выражения компонентов перемещения:

Подставив эти выражения в уравнения движения (350) и учитывая (351), придем к системе трех линейных алгебраических уравнений относительно

.

Равенство нулю определителя этой системы приводит к кубическому уравнению относительно

. Три корня этого уравнения соответствуют трем различным формам колебаний с одинаковыми числами узловых окружностей и образующих, но с различными соотношениями между

.

В отличие от пластинок, где наименьшие собственные частоты соответствуют формам колебаний без узловых линий, в оболочках, закрепленных так, что деформация их без растяжения срединной поверхности невозможна, наименьшие частоты имеют колебания с узловыми линиями. Это объясняется тем, что формы колебаний без узловых линий связаны со значительными деформациями в срединной поверхности оболочки.

Вязкое трение

В этом случае возникает сопротивление движению, которое пропорционально его скорости. При этом сила сопротивления описывается выражением

, (14)

где k- коэффициент пропорциональности.

Примером системы, работающей в условиях вязкого трения, может служить гидравлический амортизатор (рис.15), который создаёт сопротивление движению поршня, зависящее не от перемещения (как это свойственно упругим связям), а от скорости и пропорционально её первой степени (14). Подобные устройства применяются, например, в конструкциях автомобильной подвески. Гидравлический амортизатор состоит из одного или нескольких цилиндров с поршнями или из камеры, в которой может вращаться крыльчатка. Цилиндры и камера наполнены амортизационной жидкостью. При движении поршней или крыльчатки эта жидкость продавливается через калиброванные отверстия; этим создаётся сопротивление, по характеру близкое к вязкому. В формуле (14) R- это сила, действующая на амортизатор, а вязкая реакция амортизатора на колеблющееся тело имеет противоположное направление.

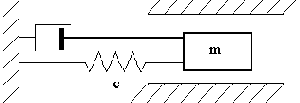
Рис. 15

Дифференциальное уравнение движения в рассматриваемом случае таково:

, (15)

или

, (16)

где

;

Для рассматриваемого линейного дифференциального уравнения с постоянными коэффициентами характеристическое уравнение имеет вид

Обозначим

Тогда решение уравнения (16) определяется формулой

(17)

или

, (18)

где

;

Следовательно, при наличии вязкого трения движение груза описывается непериодическим законом (рис. 16).

Тем не менее часто это движение называют периодическими затухающими колебаниями, несмотря на очевидную невозможность совмещения понятий "периодические" и "затухающие".

Рис. 16

Под периодом

этих колебаний понимают время между двумя максимальными смещениями:

. (19)

Величину

называют угловой частотой затухающих колебаний.

Отношение двух последовательных максимальных отклонений от положения равновесия

. (20)

Значит, последовательные максимальные отклонения системы от равновесного положения (амплитуды колебаний) представляют собой члены геометрической прогрессии со знаменателем, равным

. Чаще рассматривают не отношение двух последовательных амплитуд, а логарифм этого отношения, который называют логарифмическим декрементом колебаний:

. (21)

В металлических конструкциях без специально введенных элементов трения логарифмический декремент составляет обычно от нескольких сотых до десятых долей единицы.

Если колебания затухают медленно и отношение двух последовательных амплитуд

близко к единице, то

,

где

;

.

Таким образом, при малом затухании логарифмический декремент примерно равен отношению изменения амплитуды колебаний за период

к амплитуде

А.

Так как логарифмический декремент колебаний

,

то

.

Подставляя значение n2 в формулу для

, установим связь между величинами

. (22)

Из (22) следует, что даже при значительном затухании частота

затухающих колебаний мало отличается от частоты

собственных колебаний соответствующей системы без трения. Например, при сравнительно большом затухании, когда каждый следующий размах вдвое меньше предыдущего (

), частота

лишь на 0,6 % меньше, чем

. Таким образом, можно считать, что трение практически не влияет на частоту колебаний и

.

Определим постоянные интегрирования в решении уравнения затухающих колебаний (17). Обозначим смещение и скорость в начальный момент времени t0=0 через x0 и

соответственно. После подстановки в (17) получим

x0=C1;

,

тогда

C1=x0;

,

и решение уравнения (16) , удовлетворяющее начальным условиям, имеет вид

(23)

Пример 5. Амплитуда собственных колебаний за один период уменьшилась в два раза.Определить логарифмический декремент колебаний и изменение собственной частоты вследствие затухания.

Решение.

Логарифмический декремент колебаний:

;

,

откуда

.

Собственная частота колебаний:

,

т. е. изменение собственной частоты вследствие затухания составляет 0,6 %.

Влияние цепных усилий

Ранее продольная сила считалась заданной и не зависящей от перемещений системы. В некоторых практических задачах сопровождающая процесс поперечных колебаний продольная сила возникает вследствие изгиба балки и носит характер реакции опоры. Рассмотрим, например, балку на двух шарнирно-неподвижных опорах. При её изгибе возникают горизонтальные реакции опор, вызывающие растяжение балки; соответствующее горизонтальное усилие принято называть цепным усилием. Если балка совершает поперечные колебания, то цепное усилие будет изменяться во времени.

Если в мгновение t прогибы балки определяются функцией

, то удлинение оси можно найти по формуле

Соответствующее цепное усилие найдём при помощи закона Гука

Подставим этот результат в (215) вместо продольной силы N

(с учётом знака)

. (220)

Полученное нелинейное интегродифференциальное уравнение

упрощается при помощи подстановки

, (221)

где

безразмерная функция времени, максимальное значение которой можно положить равным любому числу, например, единице;

амплитуда колебаний.

Подставляя (221) в (220), получим обыкновенное дифференциальное уравнение

, (222)

коэффициенты которого имеют следующие значения:

;

Дифференциальное уравнение (222) является нелинейным, следовательно, частота свободных колебаний зависит от их амплитуды.

Точное решение для

частоты поперечных колебаний

имеет вид

где

частота поперечных колебаний, вычисленная без учёта цепных усилий;

поправочный коэффициент, зависящий от отношения амплитуды колебаний

к радиусу инерции поперечного сечения

; величина

приводится в справочной литературе.

При соизмеримости амплитуды и радиуса инерции поперечного сечения поправка к частоте становится значительной. Если, например, амплитуда колебаний стержня круглого сечения равна его диаметру, то

, и частота почти в два раза больше, чем в случае свободного смещения опор.

Случай

соответствует нулевому значению радиуса инерции, когда изгибная жёсткость балки исчезающе мала - струна. При этом формула для

даёт неопределённость. Раскрывая эту неопределённость, получим формулу для частоты колебаний струны

Эта формула относится к случаю, когда в положении равновесия натяжение равно нулю. Часто задачу о колебаниях струны ставят в других предположениях: считают, что перемещения малы, а растягивающая сила задана и остаётся неизменной в процессе колебаний.

При этом формула для частоты имеет вид

где N - постоянная растягивающая сила.

Влияние постоянной продольной силы

Рассмотрим случай, когда колеблющаяся балка испытывает действие продольной силы N, величина которой не меняется в процессе колебаний. В этом случае уравнение статического изгиба усложняется и приобретает вид (при условии, что сжимающая сила считается положительной)

Полагая

и считая жёсткость постоянной, получаем уравнение свободных колебаний

. (215)

Принимаем по-прежнему частное решение в виде

Тогда уравнение (215) распадается на два уравнения:

Первое уравнение выражает колебательный характер решения, второе определяет форму колебаний, а также позволяет найти частоты. Перепишем его таким образом:

(216)

где K определяется формулой (196), а

. (217)

Решение уравнения (216) имеет вид

где

Рассмотрим случай, когда оба конца стержня имеют шарнирные опоры. Условия на левом конце

дают

. Удовлетворяя те же условия на правом конце, получим

Приравнивая нулю определитель, составленный из коэффициентов при величинах

, приходим к уравнению

или

. (218)

Корни этого частотного уравнения:

Следовательно, собственная частота определится из уравнения

Отсюда при учёте (217) находим

. (219)

При растяжении

частота увеличивается, при сжатии

уменьшается. Когда сжимающая сила N приближается к критическому значению, корень стремится к нулю.

Влияние произвольно заданных сил неупругого сопротивления

Рассмотрим общий случай, когда сила неупругого сопротивления является некоторой нелинейной функцией скорости:

Ввиду сложности точного учёта влияния такой силы ограничимся приближённым, но дающим удовлетворительную точность простым приёмом. Заменим силу R эквивалентной силой вязкого сопротивления:

и определим коэффициент k из условия равенства работ, произведённых силами R и

за период колебаний.

При этом придётся ещё ввести определённое предположение о характере колебательного процесса. При действии гармонической возмущающей силы естественно предположить, что и в общем случае сил неупругого сопротивления колебательный процесс описывается законом (109). Удобнее сместить начало отсчёта времени с таким расчётом, чтобы закон колебаний принял более простой вид

(116)

и потребовать равенства указанных работ за полупериод

), в течение которого скорость (а вместе с ней и силы

) сохраняет постоянный знак.

Тогда элементарная работа эквивалентной силы

. (117)

Подставляя значение

, получим

и соответственно этому работа силы

за период равна

. (118)

Аналогично должна быть представлена работа, совершаемая заданной нелинейной силой неупругого сопротивления. Положим, что указанные действия выполнены и определён эквивалентный коэффициент

(как правило, его величина окажется зависящей от амплитуды колебаний A). Подставим найденное выражение

в решение (110):

(119)

Отметим, что неизвестная амплитуда A входит в обе части этого равенства. Определив из (119) зависимость амплитуды от частоты колебаний p, можем построить кривую, подобную кривым на рис. 45,а.

Проследим сказанное выше на примере сил неупругого сопротивления, заданных в виде

. (120)

Аналогично (117) элементарная работа силы R

Если сюда подставить (116), то получим

и работа силы R за период равна

Обозначим входящий в это выражение интеграл через S, тогда

(121)

Приравняем (118) и (121):

Отсюда находим эквивалентный коэффициент вязкого сопротивления

который следует подставить в соотношение (119), и тогда из последнего можно определить амплитуду колебаний.

Влияние трения на свободные колебания системы с n степенями свободы

Дифференциальные уравнения движения изменятся, если учесть, что при колебаниях возникают силы трения. Рассмотрим случай, когда силы трения линейно зависят от скоростей точек системы (вязкое трение).

Дифференциальные уравнения (31) в этом случае принимают вид

(55)

или в матричной форме

где

- (56)

матрица демпфирования.

Решение уравнений (55) будем искать в виде

. (57)

После подстановки (57) в (55) получим однородную систему алгебраических уравнений относительно амплитуд колебаний

, которая в матричной форме выглядит так:

. (58)

Ненулевое решение системы (58) возможно тогда и только тогда, когда её определитель равен нулю, что приводит к частотному уравнению

. (59)

Если все элементы матрицы демпфирования (56) неотрицательные, то вещественные части всех корней характеристического уравнения - отрицательные. При этом среди корней уравнения (59) могут оказаться отрицательные вещественные корни, каждому из которых, согласно (57), соответствует монотонное затухающее движение неколебательного характера. Наряду с этим, среди корней могут оказаться и комплексные сопряжённые корни вида

;

. Им соответствует затухающее колебательное движение, описываемое выражением

Общее решение задачи получится как результат наложения всех частных решений.

Влияние вязкого трения

Общее решение. Основное уравнение вынужденных колебаний с учётом вязкого трения принимает вид

(106)

где

Оно отличается от соответствующего уравнения при свободных колебаниях наличием правой части, а от уравнения вынужденных колебаний системы без трения - наличием второго слагаемого в левой части. Для получения общего решения воспользуемся способом, который применялся выше при решении подобной задачи для n = 0.

Пусть к системе с одной степенью свободы в момент времени

прикладывается мгновенный импульс; последующий колебательный процесс можно описать уравнением

(107)

Определим постоянные А и

из условий начала движения: при

должно быть Х=0,

Первое условие даёт

Из второго условия найдём

где

Таким образом, свободные колебания, вызванные импульсом S, описываются законом

и носят затухающий характер.

Как и выше, будем рассматривать возмущающую силу

в виде последовательности бесконечно малых импульсов

. Тогда общее решение задачи о действии силы F(t) принимает вид

, (108)

причём закон изменения силы F(t) может быть любым.

Гармоническая возмущающая сила. В практически важном случае действия гармонической силы

решение (108) даёт

(109)

где

(110)

(111)

Введём, как и выше, динамический коэффициент

(112)

Динамический коэффициент

не обращается в бесконечность ни при каких значениях частоты возмущения p; этим найденный результат существенно отличается от решения, полученного выше без учёта неупругого сопротивления. Зависимость

от отношения частот

при различных значениях отношения

приведена на рис. 45,a. Максимум динамического коэффициента несколько смещён в сторону от абсциссы

Однако это смещение мало, и можно приближённо определять

подставляя в (112)

т.е.

Отсюда видно, что максимум динамического коэффициента обратно пропорционален коэффициенту затухания n.
Из графиков (рис.45,a) следует, что силы вязкого сопротивления оказывают заметное влияние только в околорезонансной области. Это позволяет в удалении от резонанса принимать для

кривую, построенную без учёта вязкого сопротивления (рис. 41,a), а во всей околорезонансной области принимать

Рис. 45

Рассмотрим вопрос о "запаздывании" колебаний. Фазовый угол

определяется (111) и зависит от отношения частот

(рис. 45,б).

Как видно, при малых частотах p угол

невелик. При резонансе

фазовый угол равен

, т.е. в те мгновения, когда сила максимальна, перемещение равно нулю. При высоких частотах фазовый угол близок к

, т.е. максимуму силы соответствует максимум перемещения.

Действие периодических импульсов. В качестве исходного выражения примем вместо (104) закон свободных затухающих колебаний

. (113)

Дифференцируя, получим выражение скорости

.

Начало отсчёта совместим с временем

(рис.44,б). Для мгновения

можно записать

;

.

В мгновение

перемещение и скорость вновь равны

(114)

где S- величина импульса.

Из (114) находим

(115)

Вычислив

, можно по (113) найти решение х.

Особый интерес представляют резонансные режимы, при которых период импульсов T в целое число раз больше собственного периода колебаний

. Обозначим это число через

.

Тогда

,

и по (115) находим

;

.

При малых значениях

можно считать

т.е.

,

и решение имеет вид

.

Наибольшее значение (резонансная амплитуда) приблизительно составляет

,

т.е. оказывается обратно пропорциональным коэффициенту вязкого сопротивления (как и в случае гармонического возмущения). Коэффициент повторности при резонансе получим, разделив

на амплитуду колебаний, вызванных однократным ударом

,

т.е. с увеличением r (уменьшением частоты импульсов) резонансные амплитуды убывают.

Вынужденные колебания систем с распределенными параметрами

Рассмотренные выше (см. подразд.2.4) три способа решения задачи о вынужденных колебаниях систем с несколькими степенями свободы пригодны и для анализа колебаний систем с распределенной массой. Выбор способов обусловлен характером возмущающих сил: при гармоническом возмущении удобнее первый способ, а при произвольно заданном возмущении - третий.

Главная сайта