Аннотация
В данной работе рассматривается новый метод маскировки программ. Приводится теоретическое обоснование метода. Демонстрируются преимущества метода по сравнению с уже известными.
Генерация несущественного кода
В маскируемую функцию добавляется большое количество несущественного кода. Несущественный код строится таким образом, что его свойства точно известны маскирующему компилятору. Например, в случае использования алиасов в несущественном коде при генерации кода одновременно строится и точное множество абстрактных ячеек памяти для каждого обращения по указателю.
Этап генерации несущественного кода состоит из следующих подэтапов:
Генерация пула типов.
Генерация пула переменных.
Генерация несущественного кода.
Генерация пула типов. Подготавливаются определения типов, которые затем будут использоваться в холостом коде. Типы для холостого кода строятся одним из следующих способов:
Непосредственно используются типы, определённые в маскируемой программе.
Используются встроенные типы.
Из встроенных типов и типов, определённых в маскируемой программе, путём встраивания в шаблонные типы маскирующего компилятора. Например, из типа t, определённого в маскируемой программе, могут быть построены типы массива элементов типа t, списки, деревья с элементами типа t.
Модификацией структурных типов, определённых в маскируемой программе.
Для каждого типа, добавляемого в маскируемую программу, в маскирующем компиляторе строится класс-реализатор, на который возлагаются все функции по генерации инструкций для манипуляций с этим типом. Класс-реализатор должен удовлетворять интерфейсу TypeImplementer, который приведён на рис. 6.
Каждая несущественная переменная, добавленная в маскируемую функцию, в маскирующем компиляторе представлена классом, реализующим интерфейс VarImplementer, который показан на рис. 7.
Генерация пула переменных. Для генерации пула "холостых" переменных используются типы, построенные на предыдущей стадии. Переменные размещаются как на уровне локальных переменных функции, так и на уровне глобальных переменных.
Генерация несущественного кода. Для генерации несущественного кода используются множества операций, которые были получены с помощью методов getBinaryOps, getUnaryOps, getAssignOps интерфейса TypeImplementer.
Инструкции несущественного кода размещаются в базовых блоках вперемешку с инструкциями исходной функции и управляющими инструкциями.
interface TypeImplementer { public boolean requiresGlobalInit(); public boolean isSimple(); public boolean isUsable(); public MIFInstr emitType(MIFInstr p); public VarImplementer newVar(); public Set getBinaryOps(); public Set getUnaryOps(); public Set getAssignOps(); }
Рис. 6. Интерфейс для реализатора типов
interface VarImplementer { public TypeImplementer getType(); public MIFElem emitGlobalDecl(MIFElem p); public MIFElem emitLocalDecl(MIFElem p); public MIFElem emitInit(MIFElem p); public MIFElem emitFini(MIFElem p); }
Рис. 7 Интерфейс для реализатора переменных
"Перемешивание" управляющих инструкций. Управляющими инструкциями назовём инструкции функции, выполняющиеся при вычислении возвращающих предикатов и счётчиков, то есть инструкции, необходимые для того, чтобы расширенный граф потока управления замаскированной программы всегда выполнялся как граф потока управления исходной функции. На этом шаге все управляющие инструкции передвигаются на как можно большее расстояние от точки в программе, в которую они были изначально помещены. Границы, в пределах которых можно двигать инструкции, определяются зависимостями по данным управляющих инструкций друг от друга и зависимостями по управлению.
Общее описание метода маскировки
Метод ММ применяется к функциям маскируемой программы по отдельности, при этом структура маскируемой программы в целом не изменяется. Для изменения структуры маскируемой программы могут применяться стандартные методы открытой вставки и выноса функции, рассмотренные в [8], которые, однако, не являются частью предлагаемого метода маскировки.
При маскировке каждой функции ММ использует, наряду с локальными несущественными переменными, глобальные несущественные переменные, которые формируют глобальный несущественный контекст. В маскируемую программу вносятся несущественные зависимости по данным между существенным и несущественным контекстом функции. Наличие глобального несущественного контекста, совместно используемого всеми замаскированными функциями, приводит к появлению в замаскированной программе зависимостей по данным между всеми функциями и глобальными переменными.
Метод ММ состоит главным образом из преобразований графа потока управления. В результате граф потока управления замаскированной программы значительно отличается от графа потока управления исходной программы. Метод не затрагивает структур данных исходной программы, но вносит в замаскированную программу большое количество несущественных зависимостей по данным. В результате, замаскированная программа значительно сложнее исходной как по управлению, так и по данным.
Мы предполагаем, что перед маскировкой были выполнены все стандартные шаги анализа программы: лексический, синтаксический, семантический, анализ потока управления (построение графа потока управления и деревьев доминирования и постдоминирования) и консервативный глобальный анализ потоков данных (достигающие определения и доступные выражения с учётом возможных алиасов). Дополнительно может быть выполнено профилирование дуг, результаты которого учитываются в преобразованиях клонирования дуг и развёртки циклов.
Общая идея метода может быть охарактеризована следующим образом.
Во-первых, значительно увеличить сложность графа потока управления, но так, чтобы все дуги графа потока управления, внесённые при маскировке, проходились при выполнении программы.
Это позволяет преодолеть основную слабость "непрозрачных" предикатов.
Во-вторых, увеличить сложность потоков данных маскируемой функции, "наложив" на неё программу, которая заведомо не влияет на окружение маскируемой функции и, как следствие, не изменяет работы программы. "Холостая" функция строится как из фрагментов маскируемой функции, семантические свойства которых заведомо известны, так и из фрагментов, взятых из библиотеки маскирующего транслятора. Чтобы затруднить задачу выявления холостой части замаскированной функции используются языковые конструкции, трудно поддающиеся анализу (указатели) и математические тождества.
Маскировку можно разбить на несколько этапов:
Увеличение размера графа потока управления функции. На этом этапе выполняются различные преобразования, которые изменяют структуру циклов в теле функции, а также клонирование базовых блоков. Разрушение структуры графа потока управления функции. На этом этапе в граф потока управления вносится значительное количество новых дуг. При этом существовавшие базовые блоки могут оказаться разбитыми на несколько меньших базовых блоков. В графе потока управления могут появиться новые пока пустые базовые блоки. Цель этого этапа - подготовить место, на которое в дальнейшем будет внесён несущественный код. Генерация несущественного кода. На этом этапе пустые базовые блоки графа потока управления заполняется инструкциями, не оказывающими влияния на результат, вырабатываемый программой. Несущественная, "холостая" часть пока никак не соприкасается с основной, функциональной частью программы. "Зацепление" холостой и основной программы. Для этого используются как трудноанализируемые свойства программ (например, указатели), так и разнообразные математические тождества и неравенства.
"Перемешивание" программ
На предыдущих этапах граф потока управления функции был значительно увеличен в размерах, затем в него было добавлено большое количество несущественного кода. И предикаты, добавленные в расширенный граф потока управления для моделирования исходного графа потока управления, и несущественный код используют множество переменных, не пересекающихся с основными переменными маскируемой функции. В результате функция может быть расслоена на существенную и несущественную часть, хотя это может быть и затруднено необходимостью проведения анализа указателей.
Чтобы затруднить отделение несущественной части замаскированной функции в неё добавляется большое количество искусственных зависимостей по данным между существенной и несущественной частью. Для этого в настоящее время используются булевские, теоретико-числовые и комбинаторные тождества, а также массивы и динамическе структуры данных.
Булевские тождества. Булевские тождества применяются для усложнения булевских выражений, которые определяют условные переходы. В отличие от других видов тождеств, булевские тождества произвольной сложности легко могут получаться автоматически. Рассмотрим в качестве примера основной метод получения булевских тождеств, реализованный в настоящее время.
Булевские тождества произвольной сложности могут быть получены из булевских тождеств относительно простой структуры при помощи набора эквивалентных преобразований. Пусть мы хотим составить булевское тождество с переменными v1, v2, ..., vk, среди которых есть как переменные исходной функции, так и несущественные переменные, внесённые при маскировке. Пусть e - выражение, подвергаемое усложнению. Тогда строится выражение


Такой метод получения булевских тождеств аналогичен методу получения непрозрачных предикатов, рассмотренному в работе [8], но в данном случае использование тождеств не приводит к появлению недостижимой дуги графа потока управления, которая достаточно легко может быть обнаружена.
Поэтому использование булевских тождеств в нашем случае обнаруживается значительно сложнее.
Комбинаторные тождества. Все рассматриваемые далее тождества, как комбинаторные, так и теоретико-числовые взяты, в основном, из [3]. Рассмотрим в качестве примера следующее биномиальное тождество

Тождество может использоваться следующим образом: в качестве n берётся несущественная переменная, принимающая целые значения в небольшом интервале (например, от 0 до 5). Генерируются инструкции, вычисляющие сумму биномиальных коэффициентов и помещающие результат во временную переменную, для определённости @1. Генерируется инструкция сдвига, вычисляющая 2n и помещающая результат в другую временную переменную, например @2. Далее в исходной функции выбирается аддитивное целое выражение, результат которого сохраняется в некоторой временной переменной, например, @3, и строится новое выражение @1 + @3 - @2. Это выражение всегда будет равно выражению @3, но содержит зависимость по данным от переменной n.
Некоторые другие тождества, которые могут использоваться аналогичным образом, приведены ниже.

Теоретико-числовые тождества. В качестве примера рассмотрим известную малую теорему Ферма.
ap-1

для любого целого

Другие теоретико-числовые тождества, которые также могут использоваться для внесения зависимостей по данным, приведены ниже. Обобщением малой теоремы Ферма является теорема Эйлера:

где n и x произвольные целые числа,

(n-1)!

тогда и только тогда, когда n - простое число.
Использование массивов и динамических структур данных. Динамические структуры данных могут использоваться и для создания искусственных зависимостей по данным. Главный расчёт здесь делается на то, что в настоящее время не существует удовлетворительного алгоритма анализа алиасов, возникающих при использовании указателей и индексов массивов.
В качестве простейшего способа можно предложить размещение всех локальных переменных одного типа в массиве. В тексте функции вместо имени переменной теперь будет использоваться индекс массива. Даже случаев, когда индекс всегда представляет собой литеральную константу, будет достаточно, чтобы поставить в тупик простейшие алгоритмы анализа алиасов, которые рассматривают массив как единое целое.
В момент маскировки программы известно, какие элементы массива заняты существенными, а какие - несущественными переменными. Более того, распределение несущественных переменных по массиву может выбираться произвольным образом. Это может использоваться для построения зависимостей по данным. Пусть f - функция, ставящая в соответствие произвольному целому значению некоторый индекс в массиве, по которому находится несущественная переменная. Тогда искусственные зависимости по данным строятся с помощью выражений вида vars[f(e1)] = e2 или vars[f(e1)] = vars[f(e2)]. Здесь vars - это массив переменных, e1, e2 - выражения, которые включают в себя как существенные, так и несущественные переменные.
Один из простых способов использования динамических структур данных для внесения зависимостей по данным заключается в том, что все значения переменных всех типов хранятся в списке, размещаемом в динамической памяти. Для доступа к переменным вместо их имени используется разыменование специальных указателей. Кроме того, указатели на несущественные переменные время от времени меняют своё положение в списке. В результате окажется, что все обращения к бывшим локальным переменным функции обращаются к объектам в области динамической памяти.Для разделения существенных и несущественных переменных потребуется анализ алиасов в динамической памяти, способный работать с динамическими структурами данных произвольной глубины. В настоящее время не существует такого метода статического анализа алиасов.
Этот подход проиллюстрирован на рис. 8, На котором функция содержит четыре переменных a, b, c и d. Пусть, для определённости, переменные a и b - существенные, а c и d - несущественные. В замаскированной функции вместо этих локальных переменных вводятся переменные p1 и p2, указывающие на звенья списка, размещённого в динамической памяти. Переменная a доступна как p1->prev или как p2->next, а переменная c - как p1->next или как p2->prev.

Рис. 8. Использование списков для внесения зависимостей по данным
Практическое обоснование устойчивости метода
Устойчивость замаскированной программы к автоматическому анализу обосновывается следующими наблюдениями:
Многие методы статического анализа потоков данных не поддерживают анализ массивов с точностью до элемента. Для таких методов анализа все обращения к массиву локальных переменных будут равноправны, что приведёт к обнаружению ложных зависимостей по данным.
Для выявления зависимостей по данным между переменными глобального контекста требуется межпроцедурный анализ программы. При наличии большого числа глобальных переменных (как существенных, так и несущественных) и большого числа функции, глобальный анализ окажется либо неточным, либо будет требовать слишком много ресурсов.
То же самое замечание справедливо и для анализа указателей в область динамической памяти. Существующие методы анализа либо неточны, либо неприменимы к программам болього размера.
Устойчивость замаскированной программы к ручному анализу обосновывается следующими соображениями:
Полустатический анализ (трассировка) замаскированной программы не позволяет в ней выявить явных закономерностей, таких как никогда не выполняющиеся дуги графа потока управления или регулярно выполняющиеся блоки, как диспетчер. Отсутствие явных статистических закономерностей делает полустатический анализ значительно менее эффективным, чем в случаях, рассмотренных в работе [8].
Инструкции, обеспечивающие устойчивость замаскированной функции, распределены по всем базовым блокам функции, а не сконцентрированы на небольшом участке, как в схеме диспетчера. Поэтому демаскировка требует анализа всей функции, а не какой-то её части.
Большой размер замаскированных функций даже для относительно небольших функций исходной программы является трудным (если преодолимым) препятствием для ручного анализа.
Каждое преобразование, составляющее метод маскировки, параметризуемо в широких пределах (как правило, случайным образом). Знание, извлечённое в результате анализа одной замаскированной функции, может быть только отчасти применено к анализу другой замаскированной функции.
Граф потока управления имеет такую структуру, что его визуализация может дать неудовлетворительный результат. Алгоритмы визуализации могут отобразить граф потока управления таким образом, что это только затруднит понимание, либо вообще не смогут отобразить такой граф.
Приведённые здесь рассуждения, конечно, не заменяют формальных доказательств утверждений о трудности демаскировки. Однако следует заметить, что используемый в настоящее время подход, заключающийся в сведении какой-либо вычислительно-трудной задачи к задаче демаскировки программы, позволяет делать утверждения о трудности демаскировки методами статического анализа лишь в худшем случае.
Кроме того, в настоящее время не существует математического аппарата, пригодного для оценки сложности полустатического и динамического анализа программ, который имеет существенную эвристическую компоненту.
применения метода
В качестве примера применения предложенного метода маскировки мы выбрали небольшую программу, которая решает задачу о 8 ферзях. Текст этой программы приведён на рис. 10.

Рис. 10. Программа, решающая задачу о "8 ферзях"
Для маскировки мы выберем основную функцию queens этой программы. Граф потока управления функции queens приведён на рис. 11.

Рис. 11. Граф потока управления функции queens
Результат маскировки функции queens приведён ниже.
static void queens(int c) { int q[13u]; q[10] = 0; q[8] = 0; q[1] = (c + 7); q[4] = 0; q[7] = 0; q[2] = -1; q[11] = 0; L127: if (!q[2]) goto L128; q[11]++; q[2] = (unsigned) q[2] >> 1; goto L127; L128: q[12] = q[11]+q[2]-19; q[11] = q[11] % q[12]; L111: if (q[q[11]+4] >= 8) goto L45; q[3] = q[10]; q[q[11]+2] = ((q[8] + q[7]) + 1); q[9] = (q[10] + 1); q[1] = ((q[1] + c) + 2); q[q[11]+4] = (q[10] + 2); q[7] = ((7 + q[q[11]+2]) - q[1]); if ((v3)[q[3]] == 0) goto L94; q[4] = ((v8)[q[3]] + (v2)[((q[3] - c) + 7)]); if ((v7)[((q[3] - c) + 7)] == 0) goto L94; if (q[7] < 0) goto L96; if (q[7] 5); if ((v3)[q[9]] == 0) goto L111; if ((v7)[((q[9] - c) + 7)] != 0) goto L112; if (q[1] != 0) goto L111; if (q[4] (v6)[(q[2] + 1)]) goto L122; (v2)[(q[9] + c)] = ((v6)[q[2]] + c); q[8] = (((q[1] + q[4]) + q[9]) - 7); (v4)[(q[9] + c)] = 1; q[4] = (v8)[q[9]]; (v8)[q[9]] = 1; (v7)[((q[9] - c) + 7)] = 1; q[7] = (q[7] - 1); (v3)[q[9]] = 1; q[q[11]+5] = (q[11] + q[12]) % 13; goto L111; L45: ; }
Граф потока управления замаскированной функции приведён на рис. 12. На рисунке графа дуги, получившиеся при выполнении преобразования зацепления дуг, имеют большую толщину, а соответствующие базовые блоки выделены серым цветом.

Рис. 12. Граф потока управления замаскированной функции queens
В таблице 1 приведены метрики сложности кода для исходной функции queens и для её замаскированного варианта. У замаскированной функции значения всех метрик, кроме метрики сложности графа вызовов выше, чем у исходной функции. Принципы предлагаемого метода маскировки нашли отражение в примере следующим образом:
Массив q используется для хранения локальных переменных функции queens. В результате методы анализа потока данных, которые не различают индивидуальные элементы массива, покажут зависимости по данным между всеми операциями с массивом q, то есть между всеми локальными переменными функции queens. Для противодействия алгоритмам анализа потока данных, различающим элементы массива, для доступа к массиву q используется переменная, отображённая в элемент q[11] массива. Переменная инициализируется значением 6 в строках 9-18 функции. Для этого используется константа 32, получаемая в цикле как количество бит в целом слове, и константа 13 - количество элементов в массиве локальных переменных, которое сохраняется в элементе q[12] для последующего использования. Для анализа программы необходимо установить, что элементы q[11] и q[12] являются константами, что в данном случае возможно для методов, различающих элементы массива, но вычисление этих констант потребует интерпретации программы. Для противодействия алгоритмам продвижения констант, которые могли бы распространить константные значения q[11] и q[12] по функции, значение q[11] перевычисляется в строках 82, 129, 145. При этом значение q[11] каждый раз не изменяется. В случае, даже если в результате анализа замаскированной функции удалось выделить каждый элемент массива в отдельную переменную, замаскированная функция всё ещё содержит весь несущественный код, внесённый при маскировке. Алгоритм обнаружения мёртвого кода не даст результатов, из-за использования тождеств в строках 70-79 и 91-96, вносящих ложные зависимости по данным между основной и несущественной частью функции queens.
| Таблица 1. Изменение метрик сложности для замаскированной функции queens | ||
| метрика | исходная функция | после преобразования |
| CC (Цикломатическая сложность) [14] | 6 | 21 |
| FC (Сложность по связям) [13] | 9 | 27 |
| GC (Сложность графа вызовов) | 2 | 2 |
| SC (Структурная сложность) [13] | 3 | 24 |
| YC (Зацикленность) | 0.595 | 0.8119 |
| DC (Сложность потока данных) | 82 | 8964 |
Кроме того, дополнительные зависимости по данным и дополнительные дуги графа потока управления появляются из-за использования зацепления дуг. Первое зацепление реализовано в строках 36-38 и 131-136, а второе зацепление - в строках 70-73 и 98-100.
Разрушение структурности графа потока управления
Эта группа маскирующих преобразований включает зацепление дуг и создание псевдоциклов.
Зацепление дуг. Схема преобразования показана на рис. 3. Для преобразования выбираются две случайных дуги графа потока управления функции. При этом предпочтение отдаётся "далёким" друг от друга дугам, где расстояние измеряется как минимальное из длин двух кратчайших путей по графу от конца одной дуги к началу другой. Две выбранные дуги не должны иметь общее начало или общий конец. Ключевым для обеспечения надёжности зацепления дуг является предикат P, который в конце выполнения нового базового блока B[new] гарантирует возврат на "правильный" путь выполнения. Такой предикат мы назовём возвращающим.
До преобразования после выполнения базового блока B[from1] всегда выполнялся базовый блок B[to1], а после базового блока B[from2] всегда выполняется базовый блок B[to2]. В результате выполнения этого преобразования создаётся новый базовый блок B[new], который выполняется и после B[from1], и после B[from2]. Новый базовый блок завершается вычислением предиката P, в зависимости от которого управление передаётся либо на базовый блок B[to1], либо на базовый блок B[to2]. Предикат P должен гарантировать, что управление вернётся на ту ветвь, с которого оно пришло в блок B[new]. Методы генерации предикатов, удовлетворяющих этому требованию, будут рассмотрены ниже.
Интегрированная среда Poirot предусматривает гибкий интерфейс для подключения новых возвращающих предикатов. Добавление очередного возвращающего предиката при маскировке программы производится посредством интерфейса ReturnPredicateFactory. Интерфейс к методам генерации кода для возвращающих предикатов называется ReturnPredicateGenerator. Оба интерфейса приведены на рис. 4.
Реализованы некоторые простейшие виды возвращающих предикатов. Простейший вид возвращающего предиката - это обычная булевская переменная. Переменная может быть объявлена как на уровне локальных переменных, так и на уровне глобальных переменных.
Возвращающие предикаты могут быть построены на основе хэш-функций. Пусть хэш-функция f отображает целочисленный тип в булевский. Введём переменную v, которую будем использовать как аргумент f. Таким образом, предикат P равен f(v). Установка
 |
 |
| (a) Исходный граф. | (b) Преобразованный граф |
| Рис. 3. Схема преобразования зацепления дуг |
Рис. 4 Интерфейсы для возвращающих предикатов
значения P в true эквивалентна присваиванию переменной v любого значения x, на котором f(x) = true. Такие значения x могут браться из массива Ptrue, который индексируется произвольным выражением e. Тогда установка значения предиката P в true выполняется присваиванием v < - Ptrue[e]. Установка значения предиката P в false выполняется аналогично.Для построения возвращающих предикатов могут быть использованы динамические структуры данных, аналогично тому, как они использовались для построения счётчиков.
 |
 |
| (a) Исходный граф. | (b) Преобразованный граф |
| Рис 5. Схема построения "псевдоцикла" |
На заключительном шаге перемешивания инструкций эти инструкции будут перемещены вверх как можно выше. Во-вторых, инструкции инициализации возвращающих предикатов могут быть размещены не в самих базовых блоках B[from1] или B[from2], а в базовых блоках, из которых управление может попасть только в нужный блок.
Создание псевдоциклов. Преобразование состоит во внесении в граф потока управления функции обратной дуги. При этом контролируется, чтобы тело полученного цикла выполнялось только один раз. Схема преобразования показана на рис. 5. Здесь сцепляются дуги B[i1]->B[i2] и B[i2]->B[i3]. Предикат P, находящийся в конце базового блока B[new], должен обеспечить однократное выполнение базового блока B[i2].
Устойчивость преобразования создания псевдоцикла к анализу определяется устойчивостью возвращающего предиката. В отличие от преобразования зацепления дуг, в котором инструкции установки значения возвращающего предиката P могут быть размещены достаточно "далеко" от точки зацепления дуг, преобразование создания псевдоцикла более ограничено. Установка значения предиката P, чтобы управление покинуло псевдоцикл, не может быть вынесено из блока B[i2].
Реализация метода маскировки
В данном разделе мы рассмотрим более детально круг вопросов, связанных с реализацией предложенного метода маскировки ММ. В качестве среды реализации используется интегрированная среда Poirot.
Напомним основные обозначения, введённые ранее. Инструкции, составляющие тело функции, находятся в массиве instr, индексируемом от 0 и до Ninstr-1, где Ninstr - общее количество инструкций в теле функции. Первая инструкция в этом массиве - инструкция FUNC - пролог функции в представлении MIF, последняя инструкция - инструкция END - эпилог функции. Пусть B - массив базовых блоков этой функции, пусть для каждого базового блока i succ[i] - множество следующих за ним базовых блоков, а pred[i] - множество предшествующих ему базовых блоков, first[i] - номер первой инструкции в массиве instr, принадлежащей базовому блоку i, last[i] - номер последней инструкции в массиве instr, принадлежащей базовому блоку i, nbinstr[i] - количество инструкций в базовом блоке i. Информация о доминировании представлена для каждого блока i номером его непосредственного доминатора idom[i] и номером его непосредственного постдоминатора ipdom[i].
Информация о потоке данных программы представлена в виде ud- и du-множеств. Для аргумента j инструкции с номером i в теле функции ud[i,j] - это множество пар , в которых может модифицироваться переменная, и которые достигают данной точки функции. С другой стороны du[i,j] - это множество пар , в которых может использоваться переменная, и которые достижимы из данной точки функции.
В ud- и du-множествах также отражается собранная информация об алиасах. Для сбора информации об алиасах можно использовать понятие абстрактной области памяти. Абстрактная область памяти - именованная ячейка, доступ к которой возможен из программы одним или несколькими способами. Множество абстрактных ячеек памяти - вся память, с которой может манипулировать программа, с точки зрения алгоритма анализа алиасов. От детальности множества абстрактных ячеек памяти зависит точность выявленных указателей.
С другой стороны, чем детальнее множество абстрактных ячеек памяти, тем больше ресурсов требуется для выполнения анализа алиасов. Простейшее по структуре множество абстрактных ячеек памяти включает в себя имена всех локальных и глобальных переменных, а также специальный символ anon, обозначающий динамическую память. Здесь не делается попытки детализации структурных и массивовых типов, различения различных рекурсивных вызовов одной и той же функции, а также детализации структуры данных в динамической области.
Для каждой переменной указательного типа поддерживается множество абстрактных ячеек памяти, на которые может указывать данная переменная. Если переменная имеет кратный указательный тип, глубина разыменования указателя может быть ограничена. Обработка множества АЯП для объектов структурных и массивовых типов зависит от детальности множества АЯП. В простейшем случае, когда поля структур и элементы массивов не различаются, объект структурного или массивового типа считается указателем, если он содержит хотя бы одно поле указательного типа. Множество АЯП, на которые может указывать такой объект получается объединением всех множеств АЯП, на которые могут указывать поля структуры или элементы массива.
Информация об алиасах вычисляется с помощью стандартных алгоритмов анализа алиасов, например, описанных в [16]. После того, как для каждого указателя и для каждой точки программы вычислено множество абстрактных ячеек памяти, на которые он может указывать, эта информация переносится в ud- и du-множества. Например, если некоторая переменная v присутствует в множестве абстрактных ячеек памяти указателя p, то чтение по указателю p включается в du-цепочку переменной v, если последняя инструкция достижима из точки присваивания. В результате анализа алиасов может оказаться, что точности алгоритма недостаточно, и что множество абстрактных ячеек памяти, адресуемых некоторым указателем в некоторой точке программы, состоит из всех абстрактных ячеек памяти.
Другую сложность представляют вызовы функций.
Для выявления влияния функции на своё окружение требуется межпроцедурный анализ, являющийся весьма трудоёмким. Поэтому желательно ограничиться минимальным консервативным анализом, который исходит из следующих предположений:
Любая функция читает и изменяет все глобальные переменные.
Любая функция пытается разыменовывать любой указатель, переданный ей в качестве параметра.
После выполнения любой функции все глобальные указатели могут указывать на любые глобальные объекты, любые локальные объекты, упомянутые среди абстрактных ячеек памяти указателей-параметров, и на область динамической памяти.
Любая функция модифицирует все абстрактные ячейки памяти, на которые могут указывать указатели, переданные ей в качестве параметра.
Если среди таких абстрактных ячеек памяти есть локальные переменные указательного типа, то после выполнения функции они могут указывать на любой глобальный объект, любой локальный объект, упомянутый среди абстрактных ячеек памяти указателей-параметров функции, и на область динамической памяти.
Если функция возвращает значение указательного типа, это значение может указывать на любой глобальный объект, любой локальный объект, упомянутый среди абстрактных ячеек памяти указателей-параметров функции, и на область динамической памяти.
Современные языки содержат средства, позволяющие при объявлении функции уточнить степень влияния этой функции на окружение программы. К таким средствам относятся, например, квалификаторы типа const и restrict языка Си.
Указанные выше правила определения побочного эффекта функции отражаются на вычислении du- и ud-множеств в случае вызова функции. Дальнейшие шаги метода ММ работают с du- и ud-цепочками и не анализируют множества абстрактных ячеек памяти.
Метод ММ может использовать информацию о частотах выполнения дуг графа потока управления функции, полученную в результате профилирования. Каждой дуге графа потока управления ставится в соответствие число прохождений по ней. Поскольку каждая дуга графа потока управления однозначно идентифицируется парой номеров базовых блоков откуда она выходит и куда входит, предположим, что все частоты прохождения дуг хранятся в двумерном массиве efreq.Число efreq[i,j] равно количеству прохождений дуги B[i]->B[j]. Если такой дуги в графе потока управления не существует, положим число прохождений равным нулю. Пусть также


Список литературы
К. Арнольд, Д. Гослинг, Д. Холмс. Язык программирования Java. М.: Вильямс, 2001. Введение в криптографию. Под общей редакцией В. В. Ященко. М.: МЦМНО, 1999. Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. Основания информатики. М.: Мир, 1998. Б. В. Керниган, Д. М. Ритчи. Язык программирования Си. СПб.: Невский диалект, 2001. Д. Э. Кнут. Искусство программирования. Том 2. Получисленные алгоритмы. М.: Вильямс, 1998. Б. Страуструп. Язык программирования C++. М.: Бином, 1999. В. Чернов. Интегрированная среда для исследования "обфускации" программ. Доклад на конференции, посвящённой 90-летию со дня рождения А. А. Ляпунова. Россия, Новосибирск, 8-11 октября 2001 года. А. В. Чернов. Анализ запутывающих преобразований программ//В сб. "Труды Института системного программирования", под. ред. В. П. Иванникова. М.: ИСП РАН, 2002. B. Barak, O. Goldreich, R. Impagliazzo, S. Rudich, A. Sahai, S. Vadhan, K. Yang. On the (Im)possibility of Obfuscating Programs. LNCS 2139, pp. 1--18, 2001. S. Chow, Y. Gu, H. Johnson, V. Zakharov. An approach to the obfuscation of control-flow of sequential computer programs. LNCS 2200, pp. 144--155, 2001. C. Collberg, C. Thomborson, D. Low. A Taxonomy of Obfuscating Transformations. Departament of Computer Science, The University of Aukland, 1997. C. Collberg, C. Thomborson, D. Low. Breaking Abstractions and Unstructuring Data Structures. In Proc. of the IEEE Internat. Conf. on Computer Languages (ICCL'98), Chicago, IL, May 1998. W. A. Harrison, K. I. Magel. A complexity measure based on nesting level. In SIGPLAN notices, 16(3):63-74, 1981. M. H. Halstead. Elements of Software Science. Elsevier North-Holland, 1977. S. Henry, D. Kafura. Software structure metrics based on information flow. IEEE Transactions on Software Engineering, 7(5): 510--518, September 1981. S. Muchnick. Advanced Compiler Design and Implementation. Morgan Kaufmann Publishers, 1997. B. Schneier. Applied Cryptography: protocols, algorithms and source code in C. Second Edition. John Wiley & Sons, Inc., 1996. C. Wang. A Security Architecture for Survivability Mechanisms. PhD Thesis. Departament of Computer Science, University of Virginia, 2000. http://www.cs.virginia.edu/~survive/pub/wangthesis.pdf
G. Wroblewski. General Method of Program Code Obfuscation. PhD Thesis. Wroclaw, 2002.
Теоретическое обоснование устойчивости метода
Настоящий раздел посвящён анализу устойчивости предложенного метода маскировки.
Предварительно дадим некоторые вспомогательные определения и теоремы. Пусть

Определение 1. Пусть



Определение 2. Взаимно-однозначная односторонняя функция

Определение 3. p-приближённым алгоритмом решения оптимизационной задачи называется алгоритм, находящий решение не более чем в p раз хуже оптимального решения.
Например рассмотрим задачу S минимизации некоторого функционала f. Пусть A - p -приближённый алгоритм нахождения решения задачи S. Пусть для некоторой реализации задачи оптимальное значение функционала равно X. Тогда алгоритм A найдёт решение задачи, при котором значение f равно Y, причём будет справедливо неравенство

Определение 4. Пусть

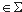


Теорема 1. Пусть


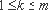
Доказательство. Введём обозначение




1. Покажем, что задача СУЩ находится в классе NP. Для этого построим булевскую формулу

Если переменная существенна, то существует такой вектор






2. Покажем, что к задаче СУЩ полиномиально сводится задача ВЫП, которая является NP-полной. Пусть





Определение 5. Пусть







Обозначим через ?f формулу, реализующую функцию f. Пусть Ф - множество формул (потенциально бесконечное) такое, что если ?f - случайно и равновероятно выбранная формула из Ф, а f - функция, которую она реализует, то случайная величина

Множество формул Ф называется семейством непрозрачных предикатов, если для любого полиномиального вероятностного алгоритма A: Ф - > {0,1} выполняются условия

Теорема 2. Если непрозрачные предикаты существуют, то P

Доказательство. Пусть P = NP. Тогда существует полиномиальный алгоритм для решения задачи выполнимости, то есть существует алгоритм A, который для любой формулы ?f за полиномиальное проверит условие f



Мы можем расширить понятие непрозрачного предиката, предположив, что область его определения может быть произвольной (например, множество всех целых чисел, представимых определённым количеством битов). Покажем, что непрозрачные предикаты могут быть реализованы и с использованием указателей, и с использованием массивов.
Теорема 3. Если булевские непрозрачные предикаты существуют, то непрозрачные предикаты, построенные на указателях, существуют.
Доказательство. Пусть f - булевский непрозрачный предикат. Пусть f:



struct s { struct s *neg; struct s *min[2]; struct s *max[2]; };
Создадим в начале работы программы в динамической памяти ссылочную структуру, показанную на рис. 9.
Здесь элемент, на который указывает Pfalse, соответствует логическому значению "ложь", а элемент, на который указывает Ptrue, соответствует логическому значению "истина".
Рассмотрим каждую булевскую операцию и поставим ей в соответствие операцию над указателями в созданной структуре данных.
xi, где xi - булевская переменная. Ей соответствует переменная pi указательного типа struct s*, которая равна либо Ptrue, либо Pfalse.



Рис. 9: Схема построения непрозрачного предиката из указателей
Таким образом, каждому булевскому выражению u мы сопоставили выражение указательного типа e. Поскольку задача определения u

Теорема 4.
Если булевские непрозрачные предикаты существуют, то и непрозрачные предикаты, построенные над массивами, существуют.
Доказательство. Пусть е - непрозрачный предикат над указателями, построенный, как показано в предыдущей теореме. Поставим ему в соответствие массив целого типа a из 10 элементов, заполненный следующим образом: int a[10] = { 5, 0, 0, 5, 0, 0, 0, 5, 5, 5 };
Указательному значению Pfalse соответствует целое значение 0, а указательному значению Ptrue - целое значение 5. Тогда выражения непрозрачного предиката, построенного на указателях, заменяются на индексные выражения по следующим правилам:
Переменная pi заменяется на переменную qi целого типа, которая может принимать значения из множества {0,5}. Выражение e->neg заменяется на выражение a[b], где b - индексное выражение, соответствующее e. Выражение e->min[f] заменяется на выражение a[b + 1 + c], где b - индексное выражение, соответствующее e, а c - индексное выражение, соответствующее f. Выражение e->max[f] заменяется на выражение \V{a[b + 3 + c]}, где b - индексное выражение, соответствующее e, а c - индексное выражение, соответствующее f.
Определение 6. Пусть f:










Теорема 5. Пусть даны m, n, f:



Доказательство. Доказательство принадлежности задачи к классу NP аналогично доказательству теоремы 1. Для доказательства NP-полноты заметим, что задача СУЩ является частным случаем данной задачи, если мы выберем I={1,...,n).
Пусть V={v1,...,vk) - множество переменных замаскированной программы. Предположим, что базовый блок представляет собой вычисление булевской функции f:


Пусть Vin






Данной оптимизационной задаче соответствует задача проверки свойств ЗАВ: дано множество булевских переменных V={v1,...,vk}, булевская функция f:







Теорема 6. Задача ЗАВ NP-полна.
Доказательство Принадлежность задачи классу NP следует из того, что для каждого i (1



Для доказательства NP-полноты покажем, как задача СУЩМНОЖ сводится к данной задаче. Пусть f - булевская функция f:


Введём m-1 новую переменную z1,...,zm-1 следующим образом: каждое вхождение xk в формулу для вычисления f заменим выражением xk v z1 v...v zm-1, а выражение - на выражение



Если переменная xk существенна для f, то переменные xk,z1,...,zm-1 окажутся существенными для f1 .
Если переменная xk несущественная для f, то все переменные xk,z1,...,zm-1 несущественны для f1. С другой стороны, если хотя бы одна переменная из множества {xk,z1,...,zm-1} окажется несущественной в f1, то и все переменные этого множества будут несущественными.
В таком случае пусть p=m-1 . Тогда, если задача ЗАВ для функции f1 , множества переменных I и значения p даёт ответ "да", отсюда следует, что все переменные xk,z1,...,zm-1 несущественны, а если ответ "нет", то все эти переменные существенны.
Таким образом задача СУЩМНОЖ сводится к задаче ЗАВ, что показывает NP-полноту последней.
Рассмотрим оптимизационную задачу ЗАВ. Она состоит в нахождении такого Win

Теорема 7. Если P

Доказательство. Пусть существует такое p>1 , что существует полиномиально-ограниченный алгоритм A, который находит множество существенных переменных WinA такое, что pA=|WinA|






Рассмотрим следующую реализацию задачи СУЩ. Пусть f - булевская функция f:


Пусть [x] - минимальное целое число, не меньшее x. Введём l=m*[p] новую переменную z1,...,zl следующим образом: каждое вхождение xk в формулу для вычисления f заменим на выражение xk v z1 v ... v zl , а выражение




Обозначим через Win0 оптимальное решение оптимизационной задачи ЗАВ для формулы f, а через Win1 - оптимальное решение для формулы f1 .
Обозначим WinA решение, найденное алгоритмом A для f1.
Пусть xk - существенная переменная. Тогда Win0 таково, что 1+1




Пусть xk - несущественная переменная. Тогда Win0 таково, что 0






Заметим, что p*(m-1)< l+1 =m*[p]+1 . В зависимости от WinA, полученного полиномиальным p-приближённым алгоритмом A мы можем определить, является ли xk существенной переменной или нет. Следовательно, P=NP.
Определение 7. Назовём "мёртвыми" все инструкции, которые относятся к вычислению несущественных переменных.
Из доказанного выше немедленно следует, что задача выявления мёртвого кода в программе, состоящей из одного базового блока, NP-полна, и, более того, для любого p>1 не существует p-приближённого полиномиального алгоритма выявления мёртвого кода.
Переменные произвольных целых типов могут рассматриваться как набор переменных булевского типа. Например, переменная типа int может рассматриваться как 32 булевские переменные, для доступа к которым используются битовые операции.
Увеличение размера графа потока управления
Преобразования перестройки циклов заключаются в том, что в маскируемой функции выбираются подходящие гнёзда циклов и одиночные циклы и над ними выполняются преобразования пространства индексов. К таким преобразованиям относятся:
Понижение размерности пространства итерирования.
Повышение размерности пространства итерирования.
Изменение порядка обхода пространства итерации.
Аффинные преобразования пространства итерации.
Частичная или полная развёртка цикла.
На этапе перестройки циклов просматриваются все циклы в теле функции. Для каждого цикла проверяются достаточные условия применимости каждого преобразования, определяя таким образом множество доступных преобразований. Затем для каждого цикла программы определяется какое преобразование будет к нему применено, и выполняются преобразования циклов.
На рис. 1 приведён пример применения преобразования понижения размерности индексного пространства к функции перемножения двух матриц. Преобразование позволило перейти от трёхкратного вложенного цикла к единственному циклу.
 |
 |
| (a) функция до преобразования | (b) функция после преобразования |
| Рис. 1. Пример преобразования понижения размерности |
Преобразование клонирования базовых блоков заключается в замене последовательного выполнения двух базовых блоков (например, B[i] и B[j]) на оператор разветвления с выполнением копии базового блока B[j] на каждой из ветвей. Для этого базовый блок B[j] должен быть скопирован необходимое число раз. На рис. 2 приведена схема преобразования.
 |
 |
| (a) Исходный граф. | (b) Преобразованный граф |
| Рис. 2. Схема преобразования клонирования базовых блоков |
На рис. 2 базовый блок B[j] был размножен дважды. Базовый блок B[cond] будет содержать инструкции, необходимые для того, чтобы каждая из трёх копий базового блока B[j] выполнялась примерно с одинаковой частотой. Базовые блоки B[new1], B[new2], B[new3] также могут содержать инструкции для поддержки равномерного распределения потока выполнения по трём альтернативам.
Уже на этапе клонирования базовых блоков начинается построение параллельной "холостой" функции, которая в дальнейшем будет объединена с основной функцией для получения результирующей замаскированной функции.
Типы данных реализации счётчиков, их переменные состояния и инструкции, соответствующие операциями над счётчиками, являются частью параллельной "холостой" функции. Переменная c, которая хранит состояние счётчика, может быть создана как на уровне локальных переменных маскируемой функции, так и вынесена в статические переменные всей единицы компиляции. Последнее позволяет разделять одну и ту же переменную состояния между разными счётчиками разных функций, что полезно ещё и тем, что создаёт в замаскированной программе межпроцедурные зависимости по данным.
В настоящее время в интегрированной среде Poirot реализованы некоторые простейшие виды счётчиков, которые описаны ниже.
Счётчик по модулю. Это - простейший вид счётчика. Состояние счётчика хранится в переменной целого типа, которая размещается на уровне статических переменных единицы компиляции. Операция init заключается в записи в переменную счётчика произвольного числа, например, значения какого-либо параметра функции или глобальной переменной. Операция get заключается во взятии остатка от деления на k текущего значения переменной счётчика. Операция next заключается в прибавлении или вычитании произвольного числа, не кратного k, причём семейство операций next порождается различным выбором этого числа.
Линейный конгруэнтный счётчик. Этот вид счётчика реализует хорошо известный линейный конгруэнтный метод получения псевдослучайных чисел [5]. Операции init и get не изменяются, а операция next определяется как next(cntr)

Криптографические хэш-функции. Для реализации счётчиков могут использоваться криптографические хэш-функции, например, MD5 или SHA [17], или симметричные криптосистемы. Тогда операция next может выглядеть следующим образом next(cntr)


Динамические структуры данных. Например, может быть создан кольцевой список, который заполняется числами от 0 до k-1 в произвольном порядке. Операция get состоит в чтении значения текущего элемента списка, а операция next - в продвижении указателя на следующий элемент списка.
Дробление базовых блоков. Это преобразование заключается в том, что базовый блок достаточной длины разделяется на два или более меньших базовых блока. Дробление базовых блоков никак не отражается на коде функции и заключается в модификации вспомогательных структур, используемых для представления графа потока управления.
В настоящее время вопросы защиты
В настоящее время вопросы защиты информации приобрели первостепенную важность. Компьютерные программы могут также рассматриваться как информация, которая нуждается в защите. Защита программного обеспечения включает в себя, с одной стороны, защиту от копирования и (или) нелицензионного использования и, с другой стороны, защиту от обратной инженерии и несанкционированной модификации. В данной работе рассматривается второй аспект защиты программ.
В качестве одного из методов защиты от обратной инженерии применяется маскировка программ. Говоря неформально, маскировка программы - это такое преобразование её текста, которое полностью сохраняет её функциональность, но делает понимание, обратную инженерию и модификацию текста программы задачей неприемлемо высокой стоимости.
Задача маскировки программ может рассматриваться с нескольких позиций. С криптографической и теоретико-сложностной точки зрения задача маскировки требует выработки приемлемого формального определения. Это направление, кроме того, включает в себя разработку методов маскировки с формально доказанным уровнем безопасности.
Мы подходим к задачае с точки зрения системного программирования. При таком подходе объектами маскировки являются тексты реальных программ, состоящих из сотен функций по несколько сотен строк каждая. Замаскированные программы должны укладываться в ограничения вычислительной системы, что не может не отразиться на используемых методах маскировки. Кроме того, большой размер исходных программ означает, что применение ручного анализа программы при ее демаскировке затруднено из-за временных и стоимостных ограничений. Для демаскировки таких программ применяются инструментальные средства анализа программ и обратной инженерии, поддерживающие полный спектр существующих статических, полустатических и динамических методов анализа.
В данной работе рассматривается задача маскировки Си-программ: маскировщик берёт на входе Си-программу, и на выходе выдаёт замаскированную Си-программу. Потребуем, чтобы программы в своей работе не использовали исключения. Основываясь на результатах анализа опубликованных методов маскировки программ [8], нами был разработан новый метод маскировки, который в наибольшей степени устойчив как к статическим, так и к полустатическим методам анализа. Этот метод излагается в настоящей работе. Разработать универсальный маскировщик, который был бы применим ко всем программам и был бы устойчивым ко всем возможным методам анализа программ, невозможно [9]. В данной работе рассматривается метод маскировки программ, который, насколько это нам удалось, удовлетворяет приведённым выше требованиям. Далее в тексте этой главы предлагаемый метод маскировки программ будет называться ММ.
ММ использует некоторые маскирующие преобразования, рассмотренные в работе [8]. Тем не менее, он выполняет их в такой комбинации с новыми преобразованиями, что применение методов анализа, описанных в [8], не дает результата. Кроме того, ММ разработан так, чтобы противостоять полустатическим методам анализа программ.
В работе представлен новый метод
В работе представлен новый метод маскировки программ, который обладает следующими отличительными особенностями.
Метод существенно увеличивает сложность графа потока управления маскируемых функций за счёт клонирования и расщепления базовых блоков, а также добавления дуг, разрушающих его структурность. Метод существенно увеличивает сложность графа зависимостей по данным маскируемых функций за счёт внесения в тело функции несущественного кода. Основной код функции и введённый несущественный код зависят друг от друга по данным за счёт использования тождеств и указателей. Метод устойчив к известным методам статического анализа программ, так как, в частности, вносит в маскируемую функцию динамические структуры данных. Метод более устойчив к полустатическим методам анализа, чем другие известные методы маскировки функций, так как замаскированная функция не содержит "мёртвых" дуг в графе потока управления.
